Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.8 - Ex. 70

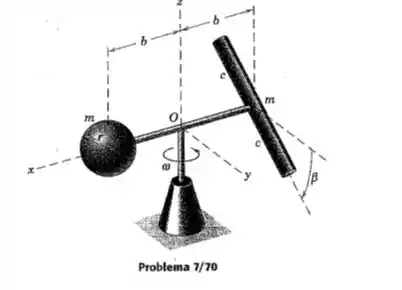
O conjunto que consiste na esfera maciça de massa m e na barra uniforme de comprimento 2c e massa igual m, gira em torno do eixo vertical z com uma velocidade angular ω . A barra de comprimento 2c tem um diâmetro que é pequeno em coparação com o seu comprimento e é perpendicular à haste horizontal na qual está soldada com a inclinação β indicada. Determine a quantidade de movimento angular combinada H o   d a   e s f e r a e da barra inclinada.

Passo 1

Antes de tudo é sempre importante calcular as componentes da velocidade angular que para este problema ω = ω k ^

Que simplifica a equação 7/11 da forma:

H o = - I x z ω i ^   - I y z ω j ^ + I z z ω k ^

Passo 2

Agora calculamos as componentes necessárias do tensor de inercia

I y z = ∫ - y z d m

y = - s c o s β e z = s * s e n ( β )

I y z = ∫ - y z d m = ∫ - c c - s c o s β s * s e n β ρ d s = ρ s e n β c o s β ∫ - c c s 2 d m =

= - ρ s e n 2 β 6 * c 3 = s e n 2 β m 6 * c 2

I x z = ∫ - x z d m = 0 pois x é fixo para esse problema.

Por fim calcularemos I z z utilizando o teorema dos eixos paralelos:

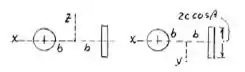
I z z = 2 5 m r 2 + m b 2 sendo r = 2 c * c o s ⁡ ( β )

I z z = 2 5 m r 2 + m b 2 = I z z = 2 5 m ( 2 c * cos ⁡ β ) 2 + m b 2

Passo 3

Voltando agora em H o nós ficamos com.

H o = - - s e n 2 β m 6 * c 2 ω j ^ + 2 5 m 2 c * cos ⁡ β 2 + m b 2 * ω k ^

H o = m ω [ 1 6 c 2 s e n 2 β j ^ + 2 5 r 2 + 1 3 c 2 c o s 2 β + 2 b 2 k ^

Resposta

H o = m ω [ 1 6 c 2 s e n 2 β j ^ + 2 5 r 2 + 1 3 c 2 c o s 2 β + 2 b 2 k ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se o cilindro hidráulico BE exerce uma força vertical F = 1,5 kN sobre a plataforma, determine a força desenvolvida nos membros AB e CD no instante θ = 90 ° . A plataforma está em repouso quando θ = 4
A caixa uniforme de 50 kg repousa sobre a plataforma para a qual o coeficiente de atrito estático é μ s = 0,5 . Se os membros-apoio têm uma velocidade angular ω = 1 rad/s, determine a maior aceleração
As quatro pás do ventilador têm uma massa total de 2 kg e momento e inércia I 0 = 0,18 kg.m² em relação a um eixo passando pelo centro do ventilador O. Se o ventilador é submetido a um momento M = 3 1
Se o motor no Problema 17.60 é desengatado do eixo assim que o volante está girando a 15 rad/s, de maneira que M = 0, determine quanto tempo vai levar antes que a resultante da força de atrito do manc
Um cabo é desenrolado de uma bobina apoiada em pequenos roletes em A e B exercendo uma força T = 300 N no cabo na direção mostrada. Calcule o tempo necessário para desenrolar da bobina 5 m de cabo se