Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.8 - Ex. 58

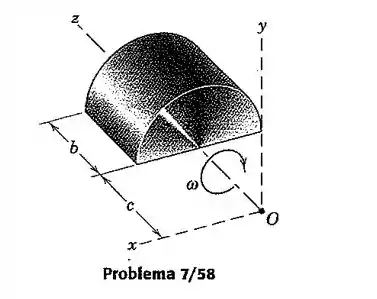
O cilindro semicircular maciço de massa m gira em torno do eixo z como uma velocidade angular  ω   conforme indicado. Determine a sua quantidade de momento angular H em relação aos eixos x-y-z.

Passo 1

Facilitaremos muito nossas contas devido o giro ser somente no eixo z, onde implica, que as componentes x e y da velocidade angular serão 0.

Teremos então:

ω = ω k ^

Passo 2

Se olharmos na equação 7/11 veremos que só precisamos calcular I x z , I y z   , I z z

I x z = ∫ - x * z d m = 0 devido a colocação dos eixos estar no centro do disco em x-z está integral será 0, pois em algum limite de integração você integra uma função impar em um intervalo simétrico.

I y z   = ∫ - y * z d m = ∭ v o l u m e - y * z * ρ d v = m 4 r 3 π * ( c + b 2 )

Ou você pode primeiramente calcular I y z     no centro de massa e utilizar o teorema dos eixos paralelos para calcular na posição dada no problema.

I z z = ∫ x 2 + y 2 d m = ∭ r 2 - z 2 ρ d v = m r 2 2

Passo 3

O momento angular fica:

H = - I y z   * ω j ^ + I z z * ω k ^

H = - m 4 r 3 π c + b 2 i ^ + m r 2 2 k ^ ω = - 4 3 π c + b 2 j ^ + r 2 k ^ r m ω

Resposta

H = - 4 3 π c + b 2 j ^ + r 2 k ^ r m ω

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O carro esportivo tem uma massa de 1,5 Mg e um centro de massa em G. Determine o tempo mais curto que ele leva para alcançar uma velocidade de 80 km/h, partindo do repouso, se o motor impulsiona somen
O carro, tendo uma massa de 1,40 Mg e centro de massa em G c , puxa um reboque carregado tendo uma massa de 0,8 Mg e centro de massa em G r . Determine as reações normais sobre ambas as rodas dianteir
O reboque com sua carga tem uma massa de 150 kg e um centro de massa em G. Se ele é submetido a uma força horizontal P = 600 N, determine a aceleração do reboque e a força normal sobre o par de rodas
A empilhadeira de 1 Mg é usada para levantar a caixa de 750 kg com uma aceleração constante de 2 m/s². Determine a reação exercida pelo solo sobre o par de rodas em A e em B. Os centros de massa para
Determine a maior aceleração com a qual a empilhadeira de 1 Mg pode levantar a caixa de 750 kg, sem fazer com que as rodas em B deixem o solo. Os centros de massa para a empilhadeira e a caixa estão l