Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 123
123. Um míssil tem a massa de (sem combustível). Se ele consome 500kg de combustível sólido a uma taxa de 20kg/s e o ejeta com uma velocidade de 2000m/s em relação ao míssil, determine a velocidade e a aceleração do míssil no instante em que todo o combustível houver sido consumido. Despreze a resistência do ar e a variação de seu peso com a altitude. O míssil é lançado verticalmente, partindo do repouso.
Passo 1
Neste tipo de problema seria importante fazer um esboço da situação que o enunciado descreve para sabermos quais são as forças que estão envolvidas no problema e a partir daí utilizar as equações desenvolvidas ao longo da seção para problemas que envolvem foguetes.
Passo 2
Um esboço do que está sendo dito no enunciado pode ser representado por:
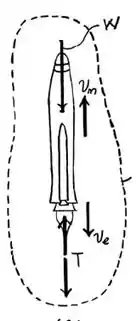
Passo 3
A massa do sistema, t segundos após ele decolar, poderá ser calculada por:
A Força peso, w, será igual a:
Passo 4
Da equação 15.28, temos que:
O instante em que todo combustível foi consumido será
Substituindo esse valor de t na equação acima, entramos:
Para obter a velocidade no instante em que todo combustível foi consumido, basta integramos a equação da aceleração atento aos limites de integração: