Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.11 - Ex. 97
97. Os dois discos idênticos estão girando livremente sobre o eixo, com velocidades angulares iguais em módulo e opostas em sentido como apresentado. O eixo por sua vez, é forçado a girar em torno do eixo vertical no sentido indicado. Prove se o eixo é flexionado conforme em ou conforme em devido à ação giroscópica.
Passo 1
Primeiro, vamos analisar o disco da esquerda:
Neste disco atua um momento no sentido anti-horário, que contribui para que ele gire.
E agora bora analisar o disco da direita, lembrando que sua velocidade angular é oposta ao primeiro disco:
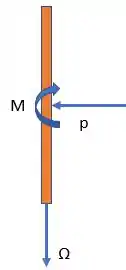
Neste disco, por sua vez atua um momento no sentido horário responsável pelo seu giro.
Passo 2
Com a análise dos discos anteriores, vamos verificar o eixo central, que no final das contas é flexionado justamente pela ação dos momentos dos nossos dois discos anteriores. Basta fazer a sobreposição dos dois momentos.
Resposta
Portanto, conseguimos verificar que o eixo é flexionado como no caso .