Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 136

Um recipiente de peso W = 1165   N é suspenso por três cabos como mostado na figura. Determine a tensão em cada cabo.

Passo 1

Vamos começar o exercício desenhando o DCL para o sistema no ponto A:

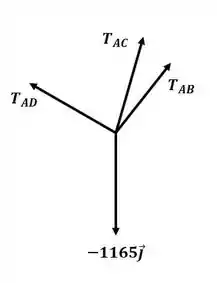
Aplicando o somatório de forças no ponto A, temos:

∑ F → A = 0

T → A B + T → A C + T → A D - 1165 j → = 0

Agora precisamos escrever os vetores tensão em termos de suas coordenadas, para isso, precisamos primeiro escrever o vetor que liga esses pontos, então:

A B → = 450 i → + 600 j →

A C → = 6 00 j → - 320 k →

A D → = - 500 i → + 600 j → + 36 0 k →

Agora, calculando o módulo desses vetores:

A B = 450 2 + 600 2 + 0 2 → A B = 750   m m

A C = 0 2 + 600 2 + - 320 2 → A C = 680   m m

A D = - 50 0 2 + 600 2 + 360 2 → A D = 860   m m

Agora podemos escrever os vetores tensão como:

T → A B = T A B . A B → A B = T A B 750 450 i → + 600 j → + 0 k → → T → A B = T A B 0,6 i → + 0,8 j →

T → A C = T A C . A C → A C = T A C 680 0 i → + 600 j → - 320 k → → T → A C = T A C 0,882 j → - 0,471 k →

T → A D = T A D . A D → A D = T A D 860 - 500 i → + 6 00 j → + 360 k → → T → A D = T A D - 0,581 i → + 0,698 j → + 0,419 k →

Passo 2

Agora substituindo os valores das tensões na equação de equilíbrio de forças do passo 1 para o ponto A, temos:

T A B 0,6 i → + 0,8 j → + T A C 0,882 j → - 0,471 k → + T A D 0,581 i → + 0,698 j → + 0,419 k → - 1165 j → = 0

Agora vamos separar as componentes i → ,   j → e k → :

0,6 T A B - 0,581 T A D = 0

0,8 T A B + 0,882 T A C + 0,698 T A D - 1165 = 0

- 0,471 T A C + 0,419 T A D = 0

Passo 3

Agora vamos isolar as componentes T A B da primeira equação do passo 2 e T A C da terceira equação:

T A B = 0,968 T A D

T A C = 0,889 T A D

Agora vamos substituir esses dois valores na segunda equação:

0,8 ( 0,968 T A D ) + 0,882 0,889 T A D + 0,698 T A D - 1165 = 0

Isolando T A D , temos:

T A D = 516,3   N

Agora substituindo esse valor nas duas primeiras equações do passo 3, temos:

T A B = 0,968 516,3 → T A B = 499,8   N

T A C = 0,889 516,3 → T A C = 459   N

Resposta

T A D = 516,3   N

T A B = 499,8   N

T A C = 459   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as forças trativas nos cabos A B , A C e A D .
Uma chapa quadrada e uniforme de aço com 360m m de comprimento de aresta e uma massa de 15k g está suspensa no plano horizontal pelos três fios verticais, como mostrado. Calcule a força trativa em cad
O eixo horizontal de aço tem uma massa de 480k g e está suspenso por um cabo vertical em A e por um segundo cabo B C que passa por baixo do eixo e está situado em um plano vertical transversal. Calcul
Duass vigas em I de aço, cada uma com uma massa de 100k g , estão soldadas em um ângulo reto e sustentadas por cabos verticais de forma que as vigas se mantêm em um plano horizontal. Calcule a força t
Por que as equações escalares de equilíbrio da estática no espaço tridimensional são em número de seis? Mais do que três equações de momento nulo podem ser consideradas nessa equação? Como e por quê?