Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.6 - Ex. 131

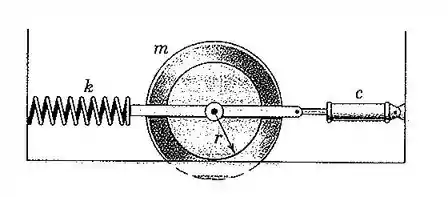
131. Calcule o fator de amortecimento ζ do sistema apresentado, se a massa e o raio de giração do cilindro escalonado são m = 8   k g e k = 135   m m , a constante de mola é k = 2,6   k N / m , e o coeficiente de amortecimento do cilindro hidráulico é c = 30   N ⋅ s / m . O cilindro rola sem deslizar sobre o raio r = 150   m m e a mola pode suportar tanto tração como compressão.

Passo 1

Bom, primeiro vamos fazer o diagrama de corpo livre do disco:

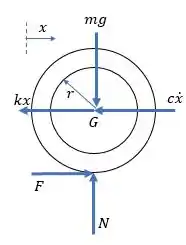
Passo 2

Fazendo o somatório de forças e momentos:

∑ F x = m x ¨

- k x - c x ˙ + F = m x ¨

F = + k x + c x ˙ + m x ¨   ( I )

↶ + ∑ M G = I - θ ¨

F ⋅ r = m k G 2 θ ¨

F = m k G 2 θ ¨ r   ( I I )

Devido o cilindro rolar sem deslizar:

x ¨ = - r θ ¨

A equação ( I I ) fica:

F = - m k G 2 x ¨ r 2

Substituindo o F da equação ( I ) nessa nova equação, temos:

- m k G 2 x ¨ r 2 = + k x + c x ˙ + m x ¨  

k x + c x ˙ + m x ¨ + m k G 2 x ¨ r 2 = 0

m 1 + k G 2 r 2 x ¨ + c x ˙ + k x = 0

Rearranjando-a:

x ¨ + c m 1 + k G 2 r 2 x ˙ + k m 1 + k G 2 r 2 x = 0

Passo 3

Lembrando que a equação genérica de movimento harmônico amortecido é:

x ¨ + c x ˙ + ω n 2 x = 0

Onde ω n é a frequência natural do sistema, então:

ω n = k m 1 + k G 2 r 2

Substituindo os valores:

ω n = 2600   N / m ( 8 k g ) 1 + ( 0,135   m ) 2 ( 0,150   m ) 2

ω n = 2600   N / m ( 8 k g ) 1 + 0,018225   m 2 0,0225   m 2

ω n = 2600   N / m ( 8 k g ) 1 + 0,81

ω n = 2600   N / m 14,48   k g

ω n = 179,56

∴ ω n = 13,40   r a d / s

Passo 4

Agora, é só calcularmos o calor de ζ pela fórmula:

ζ = c 2 ω n m 1 + k G 2 r 2

Trocando as variáveis:

ζ = 30   N ⋅ s / m 2 ( 13,40   r a d / s ) ( 8   k g ) 1 + ( 0,135   m ) 2 ( 0,150   m ) 2

ζ = 30   N ⋅ s / m 2 ( 13,40   r a d / s ) ( 8 k g ) 1 + 0,018225   m 2 0,0225   m 2

ζ = 30   N ⋅ s / m ( 214,4   k g / s ) 1 + 0,81

ζ = 30   N ⋅ s / m 388,064   k g / s

∴ ζ = 0,077

Resposta

O fator de amortecimento ζ será:

ζ = 0,077

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

132. Um oscilador linear com massa m , constante de mola k , e coeficiente de amortecimento viscoso c é colocado em movimento após ser solto de uma posição deslocada. Desenvolva uma expressão para a p
128. Determine a frequência natural f n das oscilações verticais do cilindro de massa m . A massa e o atrito do tambor escalonado são desprezíveis.
134. O instrumento sísmico mostrado está fixado no convés de um navio próximo da popa, onde a vibração induzida pela hélice é mais pronunciada. O navio possui uma única hélice com três pás que gira a
133. O cilindro A de raio r , massa m , e o raio de giração k é acionado por um sistema cabo-mola fixado ao cilindro acionador B , que oscila conforme indicado. Se os cabos não deslizam sobre os cilin
127. Determine o período τ para pequenas oscilações do conjunto composto por duas barras leves e duas partículas, cada uma de massa m . Examine a sua expressão quando o ângulo α se aproxima dos valore