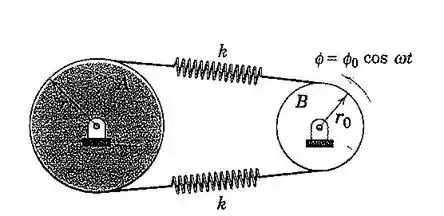
133. O cilindro de raio , massa , e o raio de giração é acionado por um sistema cabo-mola fixado ao cilindro acionador , que oscila conforme indicado. Se os cabos não deslizam sobre os cilindros, e se ambas as molas estão esticadas até o ponto em que não se afrouxem durante um ciclo de movimento, determine uma expressão para a amplitude da oscilação em regime permanente do cilindro .
Passo 1
Bom, primeiro vamos montar o diagrama de corpo livre do cilindro :
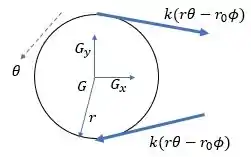
Passo 2
Fazendo o somatório de momentos em relação ao ponto :
Como o momento de inércia pode ser dado por:
Onde é a massa e é o raio de giração, então:
Rearranjando a equação e lembrando da figura que :
Passo 3
Se assumirmos que:
E substituirmos na fórmula do item anterior e resolvermos para , teremos:
Onde é a frequência natural do sistema e é dada por:
Onde é o raio de giração, é a constante elástica das molas, a massa do cilindro e o raio do cilindro.
Resposta
A expressão para a amplitude máxima é: