Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.6 - Ex. 136

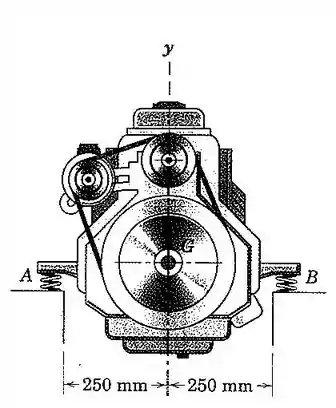
136. Um motor experimental de 220   k g está montado sobre um banco de ensaios com suportes elásticos em A e B , cada um com uma rigidez de 105   k N / m . O raio de giração em relação a seu centro de massa G é de 115   m m . Com o motor desligado, calcule a frequência natural ( f n ) y de vibração vertical e ( f n ) θ de rotação em torno de G . Se o movimento vertical é suprimido e ocorre um leve desbalanceamento em rotação, a que velocidade N o motor não deve operar?

Passo 1

Bom, já de cara a gente pode calcular o valor da vibração vertical:

( f n ) y = ω n 2 π

Como ω n = k / m

∴ ( f n ) y = 1 2 π k m

Substituindo os valores numéricos, lembrando de multiplicar o valor de k por 2 , pois há duas molas:

( f n ) y = 1 2 π 2 × 105000   N / m 220   k g

( f n ) y = 1 2 π 210000   N / m 220   k g

( f n ) y = 1 2 π 954,54

( f n ) y = 1 2 π 30,89

∴ ( f n ) y = 4,92   H z

Passo 2

Agora, vamos esquematizar como fica o motor com uma rotação em torno de G :

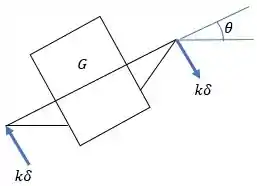
Passo 3

Para pequenos valores de θ , temos que o valor de k δ será:

k δ = 105 k N / m ⋅ ( 0,250 ⋅ θ ) = 26250 ⋅ θ   N

Fazendo o somatório de momentos em relação ao ponto G :

↶ + ∑ M G = I G θ ¨

Lembrando que o momento de inércia pode ser dado por:

I = m k - 2

Onde m é a massa e k - é o raio de giração

- 2 26250 ⋅ θ   N 0,250   m = ( 220   k g ) ( 0,115   m ) 2 θ ¨

- 13125 θ = 2,9095 θ ¨

2,9095 θ ¨ + 13125 θ = 0

∴ θ ¨ + 4551 θ = 0

Passo 4

Como sabemos que a equação genérica para um movimento harmônicos é dada por:

θ ¨ + ω n 2 θ = 0

E comparando com a equação obtida no item anterior:

ω n = 4551

∴ ω n = 67,2   r a d / s

Passo 5

Lembrando a fórmula da frequência f n :

( f n ) θ = ω n 2 π

( f n ) θ = 67,2   r a d / s 2 π

∴ ( f n ) θ = 10,7   H z

Passo 6

Calcularemos a velocidade crítica N que o motor não deve operar. Para que isso ocorra, então N deve ser igual a ω n :

N = ω n = 10,7   H z

Vamos mudar a unidade para r p m :

N = 10,7   H z × 60

∴ N = 642   r p m

Resposta

A frequência natural de vibração vertical ( f n ) y será:

( f n ) y = 4,92   H z

A frequência de rotação ( f n ) θ será:

( f n ) θ = 10,7   H z

E a velocidade crítica N :

N = 642   r p m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

131. Calcule o fator de amortecimento ζ do sistema apresentado, se a massa e o raio de giração do cilindro escalonado são m = 8k g e k = 135m m , a constante de mola é k = 2,6k N / m , e o coeficiente
135. Uma bala de 60g é disparada com uma velocidade de 300m / s contra o bloco de 5k g montado em uma viga em balanço rígida, porém leve. A bala fica alojada no bloco, o qual, em seguida, vibra com um
29. Determine o valor do coeficiente de amortecimento viscoso c , para o qual o sistema é criticamente amortecido.
33. Determine o valor do coeficiente de amortecimento viscoso c , para o qual o sistema é criticamente amortecido.