Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.6 - Ex. 135

135. Uma bala de 60   g é disparada com uma velocidade de 300   m / s contra o bloco de 5   k g montado em uma viga em balanço rígida, porém leve. A bala fica alojada no bloco, o qual, em seguida, vibra com uma frequência de 4   H z . Calcule o deslocamento máximo A durante a vibração e determine a constante de amortecimento c em N ⋅ s / m se a razão entre duas amplitudes separadas de dez ciclos completos é de 0,6 . Despreze qualquer perda de energia durante o primeiro quarto de ciclo.

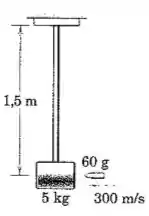
Passo 1

Bom, primeiro vamos esquematizar como fica o bloco antes e depois do impacto da bala:

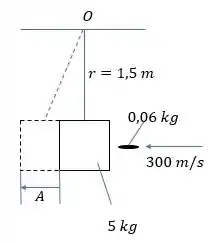
Passo 2

Agora, vamos calcular o valor da velocidade v após o impacto pela conservação do momento angular em relação ao ponto O :

H O 1 = H O 2

5   k g + 0,06   k g ⋅ v ⋅ r = 0,06   k g ⋅ 300 m / s ⋅ r

v = 0,06   k g × 300   m / s 5,06   k g

∴ v = 3,56   m / s

Passo 3

Ignorando eventuais perdas de energia após o impacto, podemos fazer a seguinte relação:

T m á x = V m á x

Onde T é a energia cinética e V é a energia potencial.

1 2 m v 2 = 1 2 k A 2

Onde k é a constante elástica da mola e k a rigidez elástica

1 2 ( 5,06   k g ) ( 3,56   m / s ) 2 = 1 2 k A 2

k A 2 = 64,13   k g ⋅ m 2 s 2   ( I )

Passo 4

Lembrando a fórmula da frequência f n :

f n = ω n 2 π = 1 2 π k m

Como sabemos que f n é 4   H z :

4   H z = 1 2 π k 5,06   k g

8 π   H z = k 5,06   k g

64 π 2   H z 2 = k 5,06   k g

k = 64 π 2 ⋅ 5,06   N / m

∴ k ≅ 3200   N / m

Substituindo o valor de k na equação ( I ) :

( 3200   N / m ) A 2 = 64,13   k g ⋅ m 2 s 2

A 2 = 64,13   k g ⋅ m 2 s 2 3200   N / m

A = 0,020   m 2

∴ A ≅ 0,141   m

Passo 5

Para uma vibração amortecida, nós temos a fórmula:

ln ⁡ x 0 x n = n ζ ω n τ d

O valor do período τ d será dado pela fórmula:

τ d = 2 π ω n 1 - ζ 2

ln ⁡ x 0 x n = n ζ ω n 2 π ω n 1 - ζ 2

∴ ln ⁡ x 0 x n = n ζ 2 π 1 - ζ 2

Substituindo os valores numéricos:

ln ⁡ 1 0,6 = ( 10 ) ζ 2 π 1 - ζ 2

0,511 = 10 ζ 2 π 1 - ζ 2

0,511 ( 10 ) ( 2 π ) = ζ 1 - ζ 2

0,00813 = ζ 1 - ζ 2

0,0000661 = ζ 2 1 - ζ 2

6,61 × 10 - 5 1 - ζ 2 = ζ 2

6,61 × 10 - 5 - 6,61 × 10 - 5 ζ 2 = ζ 2

6,61 × 10 - 5 ζ 2 + ζ 2 = 6,61 × 10 - 5

1,0000661   ζ 2 = 6,61 × 10 - 5

ζ 2 = 6,61 × 10 - 5

ζ = 6,61 × 10 - 5

∴ ζ ≅ 0,00813

Passo 6

Por fim, vamos calcular o valor da constante de amortecimento c pela fórmula:

ζ = c 2 m ω n

c = 2 m ω n ζ

Substituindo os valores, lembrando que ω n = k / m

c = 2 ( 5,06   k g ) 3200 N / m 5,06   k g ( 0,00813 )

c = ( 0,0822756   k g ) 632,41 N / m ⋅ k g

c = ( 0,0822756 ) ( 25,15 )

∴ c = 2,07   N ⋅ s / m

Resposta

O deslocamento máximo A será:

A = 0,141   m

E a constante de amortecimento c

c = 2,07   N ⋅ s / m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

31. A adição de amortecimento a um sistema massa-mola não amortecido provoca um aumento de 25 % em seu período. Determine o fator de amortecimento ξ .
34. O cilindro de 2,5k g sustentado por molas é colocado em vibração livre vertical e se observa que ele possui um período de 0,75s na parte (a) da figura. O sistema é em seguida totalmente imerso em
32. Um oscilador harmônico linear que possui uma massa de 1,10k g é colocado em movimento com um amortecimento viscoso. Se a frequência é de 10H z e se duas amplitudes sucessivas separadas de um ciclo
No exemplo 15 - 7 , qual é a razão entre a amplitude das oscilações amortecidas e a amplitude inicial após 20 ciclos?Exemplo 15 - 7 : m = 250g , k = 85N / m e b = 70g / s , T = 0,34s . A amplitude é d
27. Um pedaço de 3k g de massa de vidraceiro cai de uma altura de 2m sobre o bloco de 28k g inicialmente parado, que é apoiado por quatro molas, cada uma das quais possui uma constante k = 800N / m .