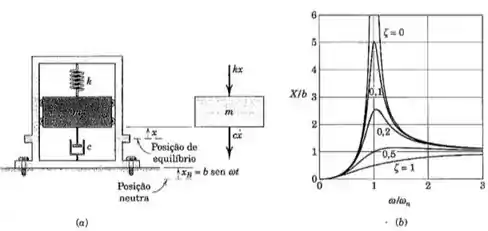
60. Desenvolva a equação de movimento para o deslocamento inercial da massa da Fig. . Comente sobre, mas sem realizar, a solução da equação do movimento.

Bom, já partindo do seguinte princípio:

Temos que:

Do texto da imagem no livro:

O que, com as relações anteriores, nos fornece:

Ao rearranjarmos deixando as variáveis correspondentes a de um lado e as correspondentes a do outro, obteremos:

E como já temos conhecimento de:

E também de que:

Então ficamos com: