Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 27

Determine a distância s que o pintor de 90 kg pode escalar sem fazer com que a escada de 4 m escorregue em sua extremidade inferior A. O topo da escada de 15 kg tem um pequeno rolo e, no solo, o coeficiente de atrito estático é 0,25. O centro de massa do pintor está diretamente acima de seus pés.

Passo 1

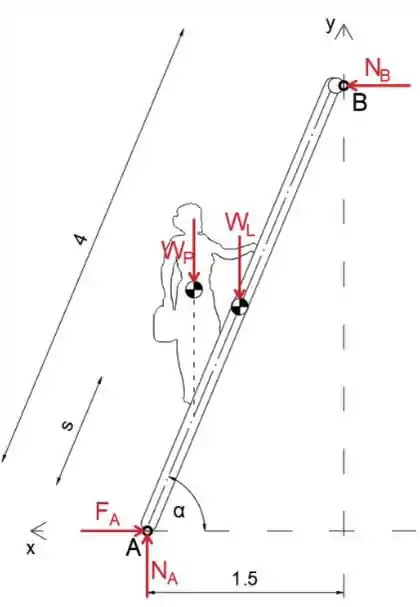
Primeiro vamos desenhar o diagrama de corpo livre da escada

Peso do pintor

W P = m P ⋅ g W P = 90 ⋅ 9.81 W P = 882.9 N

Peso da escada

W L = m L ⋅ g W L = 15 ⋅ 9.81 W L = 147.15 N

O ângulo que a escada faz com o eixo x

α = a r c c o s ⁡ 1.5 4 α = 67.98 ∘

Passo 2

Equacionando a soma das forças na direção y a zero, determinaremos a força de reação normal NA

∑ F y = 0

N A - W P - W L = 0 N A = W P + W L N A = 882.9 + 147.15 N A = 1030.05 N

Fricção máxima F A m a x é

F A m a x = μ s N A F A m a x = 0.25 ⋅ 1030.05 F A m a x = 257.51 N

Passo 3

Vamos assumir que a força FA é igual à força de atrito máxima FA max, então, ao igualar a soma dos momentos sobre o ponto B a zero, vamos determinar o comprimento máximo s em que o escorregamento não ocorre

∑ M B = 0

- 4 s i n ⁡ α ⋅ F A + 4 c o s ⁡ α ⋅ N A - 4 2 c o s ⁡ α ⋅ W L - ( 4 - s ) c o s ⁡ α W P = 0

Substituiremos F A , N A , W L , W P  e  α ´por seus valores

- 4 s i n ⁡ 67.98 ∘ ⋅ 257.51 + 4 c o s ⁡ 67.98 ∘ ⋅ 1030.05 - 2 c o s ⁡ 67.98 ∘ ⋅ 147.15 - ( 4 - s ) c o s ⁡ 67.98 ∘ ⋅ 882.9 = 0 479.54 - ( 4 - s ) ⋅ 331.03 = 0 4 - s = 479.54 331.03 4 - s = 1.45 s = 4 - 1.45

s = 2.55 m

Resposta

s = 2.55 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

8.2. Determine a força P mínima exigida para empurrar a caixa deslize plano acima. A caixa tem massa de 50k g e o coeficiente de atrito entre a caixa e o plano é μ s = 0,25
8.1. Determine a força horizontal mínima P necessária para impedir que a caixa deslize plano abaixo. A caixa tem uma massa de 50k g e o coeficiente de atrito estático entre a caixa e o plano é μ s = 0
8.4. Se o coeficiente de atrito estático em A é μ s = 0,4 e o colar em B é liso, de modo que só exerce uma força horizontal sobre o cano, determine a distância mínima x de modo que a cantoneira possa
8.5. O homem de 90k g sobe pela escada e para na posição mostrada após sentir que a escada está na iminência do deslizamento. Determine a inclinação θ da escada se o coeficiente de atrito estático ent
8.9. Se o coeficiente de atrito estático em todas as superfícies de contato for μ s , determine a inclinação θ em que os blocos idênticos, de peso W cada um, começam a deslizar.