Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 10
A placa semicircular de gira em torno de um rolamento fixo em que pode exercer um momento de atrito máximo de na placa. A força horizontal é aplicada a uma corda enrolada em torno da periferia da placa e presa em . Com , determine o ângulo máximo para o qual o equilíbrio é possível. A partir da posição determinada em , calcule a força necessária para girar o corpo no sentido anti-horário.
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar duas coisas: o valor de máximo de para que o corpo de fique em equilíbrio, considerando e momento de atrito máximo igual a ; e o valor da força necessário para que o corpo gire no sentido anti-horário a partir do ângulo determinado.
Então bora resolver! Esse exercício é bem simples, vamos começar analisando o diagrama de corpo livre da estrutura para o primeiro caso.
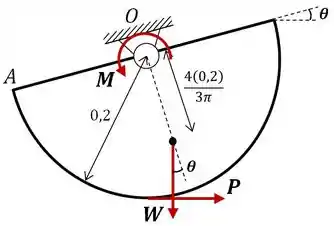
Onde:
E é o momento de atrito máximo de na placa.
Passo 2
O diagrama de corpo livre ajuda muito né?
Bom, para o caso temos que , restando apenas o peso atuando no corpo que tende a fazer a placa girar no sentido horário, então o momento de atrito está atuando no sentido anti-horário. Como foi dito que o sistema está em equilíbrio, podemos usar o somatório de momentos em torno de para determinar o ângulo :
Passo 3
De boa demais né? Para o item , vamos manter esse ângulo e descobrir a força mínima necessária para romper o atrito e a inércia e o corpo girar em sentido anti-horário.
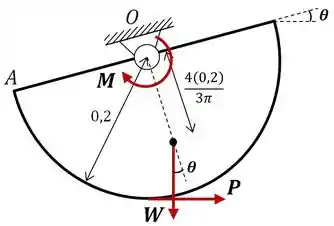
Diferente do primeiro caso, aqui a força faz o corpo girar no sentido anti-horário, então ela deve equivaler ao momento de atrito somado ao momento gerado pelo peso da placa que tendem a fazer a placa girar em sentido horário. Logo:
Falei que ia ser tranquilo né?
Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 