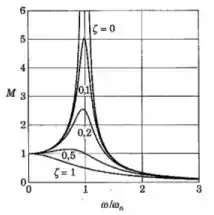
55. Um sistema massa-mola com amortecimento viscoso é forçado harmonicamente na frequência natural não amortecida ( ω / ω n = 1 ). Se o fator de amortecimento ζ é duplicado de 0,1 para 0,2 , calcule a percentagem de redução R 1 na amplitude em regime permanente. Compare com o resultado R 2 de um cálculo semelhante para a condição ω / ω n = 2 . Verifique os seus resultados examinando a Fig. 8 / 11

A redução percentual R 1 para o caso ω / ω n= 1 será de: R 1 = 50 % Já a redução R 2 para o caso ω / ω n= 2 será: R 2 = 2,42 %

Enunciado

Bom, primeiro a gente vai lembrar que a fórmula do fator de amplificação é dada por:

Onde é a frequência da força de excitação, é a frequência natural do sistema e é o fator de amortecimento.

Agora, a gente vai calcular um fator para um fator de amortecimento e , conforme pede a questão:

E calcularemos um fator para um fator de amortecimento dobrado () e :

A porcentagem de redução na amplitude será feita pela seguinte regra de . Olha só que beleza:

E a redução é dada por:

Agora, a gente vai calcular um fator para um fator de amortecimento e :

E calcularemos um fator para um fator de amortecimento dobrado () e :

E por fim, vamos calcular a redução na amplitude, pela regra de abaixo:

De modo que obtemos o valor da redução como:

A redução percentual para o caso será de:

Já a redução para o caso será: