Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas de Revisão - Ex. 109

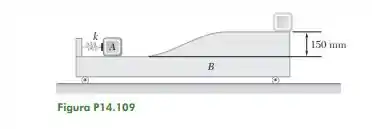
14.109. Um bloco B de 7,5 kg está em repouso e uma mola de constante k 15.000 N/m é mantida comprimida em 75 mm por um cordão. Em seguida, o bloco A de 2,5 kg é colocado defronte à extremidade da mola e cordão é cortado causando o movimento de A e B. Desprezando o atrito, determine as velocidades de A e B imediatamente após A deixar B.

Passo 1

Vamos matar mais uma?

Bom, no começo do movimento o sistema está em repouso, o que significa que o momento linear inicial é nulo, já no final do movimento tanto o A quanto B possui velocidade. A gente pode usar conservação de momento linear aqui.

0 = m A v A + m B v B  

Então

v B = - m A m B v A

Passo 2

Relacionamos v A com v B . A gente vai precisar disso. Bom, agora podemos usar conservação de energia. Veja, nesse sistema há duas energias potenciais, e as duas estão relacionadas ao bloco A. A primeira delas é a energia potencial elástica no começo do movimento, a outra é a potencial gravitacional no final do movimento.

∑ T i + V i = ∑ T f + V f

Então

1 2 k x 2 = m A g h + 1 2 m A v A 2 + 1 2 m B v B 2

Vamos substituir a relação que encontramos para v B

1 2 k x 2 = m A g h + 1 2 m A v A 2 + 1 2 m B - m A m B v A 2

Isso fica

1 2 k x 2 = m A g h + 1 2 m A v A 2 + m A 2 2 m B v A 2

Então

1 2 k x 2 = m A g h + v A 2 m A 2 + m A 2 2 m B

Então chegamos em

v A 2 = 1 2 k x 2 - m A g h m A 2 + m A 2 2 m B

Então

v A = ± 1 2 k x 2 - m A g h m A 2 + m A 2 2 m B

Vamos substituir os valores

v A = ± 1 2 ( 15000 ) 0,075 2 - ( 2,5 ) ( 9,81 ) ( 0,150 ) ( 2,5 ) 2 + 2,5 2 2 ( 7,5 )

v A = ± 4,8 m s

Mas olha para a imagem, podemos ver que o bloco A se move para direita, então esse valor é somente positivo.

v A = 4,8 m s

Passo 3

Agora podemos determinar v B .

v B = - m A m B v A

v B = - 2,5 7,5 4,8 = - 1,6 m s

Resposta

v A = 4,8 m s v B = - 1,6 m s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na talha diferencial mostrada, as duas polias superiores estão presas uma na outra para formar uma só unidade. O cabo é enrolado em torno da polia menor com sua extremidade fixada na polia de modo que
Um projétil é lançado a partir do ponto O com uma velocidade inicial de módulo v 0 = 300m / s , direcionado como indicado na figura. Calcule as componentes x , y e z da posição, velocidade e aceleraçã
Um brinquedo de parque de diversões chamado “saca-rolha” leva os passageiros de cabeça para baixo através da curva de uma hélice cilíndrica horizontal. A velocidade dos carros quando passam pela posiç
O elemento giratório em uma câmara de mistura recebe um movimento axial periódico z = z 0s e n 2 π n t enquanto está girando na velocidade angular constante θ ˙ = ω . Determine a expressão para o módu
A partícula P se desloca ao longo da curva no espaço e tem uma velocidade v = 4 i - 2 j - km / s para o instante de tempo mostrado. No mesmo instante a partícula tem uma aceleração a cujo módulo é de