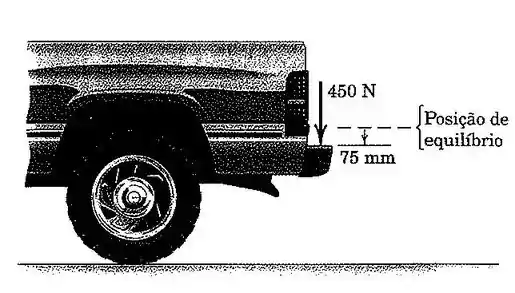
44. O proprietário de uma caminhonete de testa a ação dos amortecedores traseiros aplicando uma força constante de ao para-choque traseiro e medindo um deslocamento estático de . Após a retirada súbita da força, o para-choque sobe e em seguida desce até um máximo de abaixo da posição de equilíbrio sem carregamento do para-choque, no primeiro retorno. Considere a ação como um problema unidimensional, com uma massa equivalente igual à metade da massa do caminhão. Determine o fator de amortecimento viscoso para a extremidade traseira e o coeficiente de amortecimento viscoso para cada amortecedor assumindo que sua ação é vertical.

Agora, vamos tratar de obter o fator de amortecimento através da fórmula que o relaciona com o decrescimento logarítmico :

Depois devemos lembrar que o fator de amortecimento é dado em função do coeficiente de amortecimento viscoso e da frequência angular natural , pela seguinte fórmula:

E vamos tratar de obter a frequência natural , que está relacionada com a massa e a constante elástica por:

Para obter a massa, a questão nos diz para considerarmos apenas a metade da massa do caminhão. E como obviamente, ele tem dois amortecedores traseiros e dois dianteiros, a massa do nosso cálculo é dada por:

Agora para obter a constante elástica , basta usar a fórmula da força elástica dada pelo produto da constante elástica pela deformação . A força, nós sabemos que é igual a e o deslocamento para essa força é de . Com isso, partiu usar a fórmula:

Em seguida, uma vez que já sabemos e , vamos obter a nossa frequência natural , que é dada por:

Como já temos todos os valores que precisamos, vamos logo tratar de obter o nosso fator de amortecimento ; para apenas um amortecedor, hein. Presta atenção que a nossa massa , agora é de , metade do valor que encontramos no .