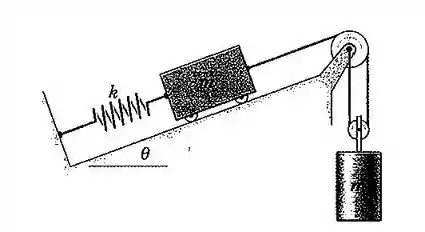
19. Calcule a frequência natural do sistema mostrado na figura. A massa e o atrito das polias são desprezíveis.

Agora, vamos fazer o diagrama de corpo livre das forças dinâmicas apenas da massa suspensa:

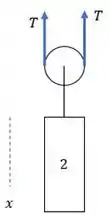
E se fizermos o somatório de forças no eixo , teremos:

Isolaremos a força :

Para resolver este problema, devemos assumir que a aceleração será metade da aceleração :

Com isso, nossa equação passa a ser:

Agora, se substituirmos a força na equação :

E vamos chamar a aceleração de :

Rearranjando a equação:

Sabemos que a fórmula genérica de um movimento harmônico é:

Onde e são constante elástica e massa genérica, respectivamente.

Agora, a gente vai calcular a frequência que foi pedida no enunciado pela fórmula: