Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 40

14.40 Em um jogo de bilhar, a bola A se desloca com uma velocidade v0 de intensidade v0 5 m/s quando ela atinge as bolas B e C, que se encontram em repouso e alinhadas como mostrado na figura. Sabendo que após a colisão as três bolas se movem nas direções indicadas e considerando as superfícies sem atrito e os choques perfeitamente elásticos (isto é, conservação de energia), determine as intensidades das velocidades vA, vB e vC.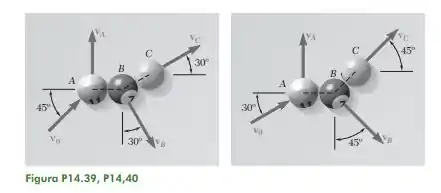

Passo 1

Primeiramente vamos escrever todas as velocidades como vetores:

v 0 → = v 0 ( cos ⁡ 30 °   i ^ + sin ⁡ 30 °   j ^ )  

v A → = v A   j ^ v B → = v B ( sin ⁡ 45 °   i ^ - cos ⁡ 45 °   j ^ ) v C → = v C ( cos ⁡ 45 °   i ^ + sin ⁡ 45 °   j ^ )

Agora vamos usar conservação de momento

m v 0 = m v A + m v B + m v C

Podemos cortar a massa

v 0 = v A + v B + v C

Vamos escrever a conservação de momento para cada componente. Para a componente i ^ temos:

v 0 cos ⁡ 30 ° = v B sin ⁡ 45 ° + v C cos ⁡ 45 °

0 , 87 v 0 = 0 , 707 v B + 0 , 707 v C

E para a componente j ^ temos:

v 0 sin ⁡ 30 ° = v A - v B cos ⁡ 45 ° + v C sin ⁡ 45 °

0 , 5 v 0 = v A - 0 , 707 v B + 0 , 707 v C

Passo 2

Vamos usar essas equações para descobrir os valores de v B e v C em termos de v A e v 0

0,87 v 0 = 0,707 v B + 0,707 v C

Vamos resolver primeiro para v B

v B = 0 , 87 v 0 - 0,7 07 v C 0,707 = 1 , 23   v 0 - v C

Agora substituímos isso em

0,5 v 0 = v A - 0,707 v B + 0,707 v C

0,5 v 0 = v A - 0,707 1,23   v 0 - v C + 0,707 v C

0,5 v 0 = v A - 0,87 v 0 + 1,414   v C

Então ficamos com

1,414 v C = 1 , 37 v 0 - v A

v C = 0,97 v 0 - 0,707   v A  

Agora substituímos esse resultado em

v B = 1,23   v 0 - v C

v B = 1,23   v 0 - 0,97 v 0 - 0,707   v A  

v B = 0,26   v A + 0 , 707 v 0

Passo 3

Agora vamos usar conservação de energia

1 2 m v 0 2 = 1 2 m v A 2 + m v B 2 + m v C 2

Podemos cortar m 2

v 0 2 = v A 2 + v B 2 + v C 2

Agora vamos substituir os valores de v C e v B

v 0 2 = v A 2 + 0,26   v A - 0,707 v 0 2 + 0,97 v 0 - 0,707   v A 2

Isso aqui vai dar

v 0 2 = v A 2 + 0 , 067 v A 2 + 0,5 v 0 2 - 0 , 18 v A v 0 + 0,94 v A 2 + 0 , 5 v 0 2 - 0 , 69 v A v 0

Agora podemos resolver para v A

2 v A 2 - v 0 v A + v 0 2 = 0

v A = 0 , 5 v 0

v A = 0 , 5 ( 5 ) = 2 , 5 m s

Consequentemente

v B = 0,26   v A + 0,707 v 0

v B = 0,26   2,5 + 0,707 ( 5 ) = 3,06 m s

E´

v C = 0,97 ( 5 ) - 0,707   ( 2,5 ) = 3,06 m s  

Resposta

v A = 2,5 m s v B = 3,06 m s v C = 3,06 m s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A trajetória de uma partícula é definida por y ²=4 k x ² e a componente da velocidade ao longo do eixo y é V y=c t e , onde ambos os k e c são constantes. Determine as componentes x e y da aceleração
Uma partícula se move ao longo da curva y = x - ( x 2 / 400 ) , se a componente da velocidade em x(vx) permanece constante e igual a 2m/s, determinar as intensidades da velocidade e aceleração quando
Um motociclista se move com uma velocidade escalar vd constante ao longo de uma trajetória. Onde em um pequeno trecho assume uma forma de curva senoidal. Determinar as componentes x e y da velocidade,
No instante mostrado, o carro A move-se ao longo da porção reta da estrada com uma velocidade escalar de 25 m/s. Neste mesmo instante, o carro B move-se ao longo da porção circular da estrada com uma
A posição de uma partícula é definida por r = t 3 i → + 2 t 2 j → + 8 t k →m , onde t é dado em segundos. Determine a intensidade da velocidade e da aceleração e o raio de curvatura da trajetória quan