Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 83
A seção axial dos dois discos circulares correspondentes é mostrada. Derive a expressão para o torque M necessário para girar o disco superior sobre o inferior fixo se a pressão p entre os discos segue a relação p = k / r², onde k é uma constante a ser determinada. O coeficiente de atrito µ é constante em toda a superfície.
Passo 1
Uma vez que a pressão não é constante (é inversamente proporcional a radins), não podemos definir a posição da força de atrito resultante a não ser usando integração
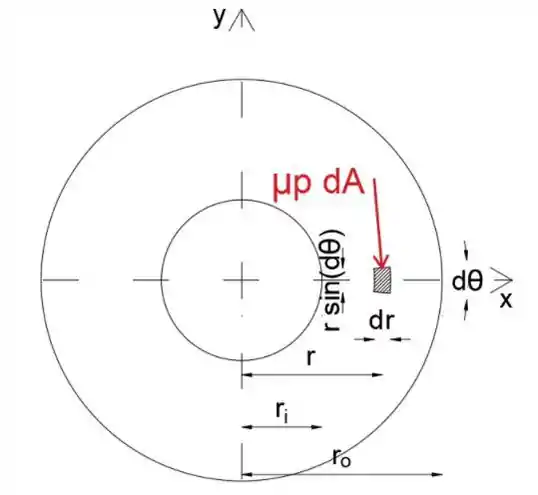
Imagine uma pequena superfície de área diferente
Uma vez que o seno de ângulo diferente é igual ao próprio ângulo, podemos escrever a expressão para dA como
Com a força dP atuando nela, que é igual ao produto da pressão p e da área dA
Substituiremos por
(2)
Então a força de atrito F atuando na superfície diferente de forma pequena será
Passo 2
O momento que o atrito da superfície diferente está causando é
Podemos substituir dF pela expressão (2)
O momento de fricção é igual à soma de todos os pequenos momentos dM diferentes ao longo do intervalo de
Vamos substituir dM pela expressão (3)
Passo 3
Agora, vamos definir a constante k
A pressão entre os discos é igual à soma de todas as pressões diferentes dP pequenas ao longo da faixa de
Substituiremos dp pela expressão(1)
Como sabemos que a pressão entre os discos é igual à força axial aplicada a eles, podemos substituir P por L
A partir da expressão acima, podemos expressar k
(5)
Finalmente, vamos substituir k pela expressão (5) na expressão (4)