Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 56

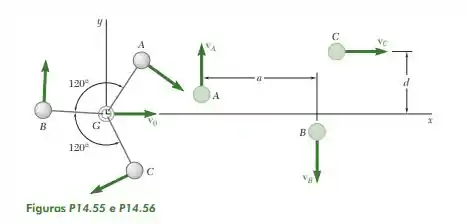
Três pequenas esferas idênticas A, B e C, que podem deslizar livremente sobre uma superfície horizontal sem atrito, estão ligadas por três fios de comprimento l que estão amarrados a um anel G. Inicialmente, as esferas giram em torno do anel que se desloca ao longo do eixo x com velocidade v0. Repentinamente, o anel se parte e as três esferas passam a se mover livremente no plano xy. Sabendo que , e , determine (a) a velocidade inicial do anel, (b) o comprimento l dos fios, (c) a taxa em rad /s com que as esferas giram em torno de G.

Passo 1

Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.

Pela conservação de momento angular, temos:

Após o choque, ficamos com:

Igualando os H:

Aplicando a conservação de energia:

Passo 2

Para a letra b, basta substituir na fórmula do

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A posição de uma partícula é definida por r = t 3 i → + 2 t 2 j → + 8 t k →m , onde t é dado em segundos. Determine a intensidade da velocidade e da aceleração e o raio de curvatura da trajetória quan

A posição de uma partícula é definida por r = 2 sen ⁡ π 4 t i → + 2 cos ⁡ π 4 t j → + 3 t k →m , onde t é dado em segundos. Determine as intensidades da velocidade e da aceleração em qualquer instante

A velocidade de uma partícula é dada por v = 16 t 2 i + 4 t 3 j + 5 t + 2 k m/s, onde t é dado em segundos. Se a partícula está na origem quando t = 0 , determine a intensidade da aceleração da partíc

Uma partícula move-se ao longo da trajetória y 2 = 4 x com uma velocidade escalar constante de v = 4 m / s . Determine as componentes x e y da velocidade e aceleração quando a partícula está em x = 4

A velocidade de uma partícula é v = 3 i + 6 - 2 t j m / s , onde t é dado em segundos. Se r = 0 quando t = 0 , determine o deslocamento da partícula durante o intervalo de tempo t = 1 s a t = 3 s .