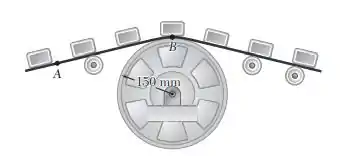
Uma série de pequenos componentes de máquina movidos por uma correia transportadora passa sobre uma polia esticadora de de raio. No instante mostrado na figura, a velocidade angular da polia esticadora é de no sentido horário. Determine a aceleração angular da polia para a qual a intensidade da aceleração total do componente de máquina em é de .

Fala aí, galerinha. Tudo certo? Bora para mais uma questãozinha de Dinâmica. Neste problema temos que determinar a aceleração angular da polia para a qual a intensidade da aceleração total do componente de máquina em é de .

Para isso, vamos utilizar a relação da aceleração tangencial, dada por:

Em seguida, vamos determinar a aceleração normal. Sabemos que ela é dada por:

Agora que encontramos as acelerações normal e tangencial, vamos determinar a aceleração angular da polia a partir da relação para a aceleração total, dada por:

Substituindo:

É isso, galerinha. Bora praticar mais pra ficar craque!