Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 53
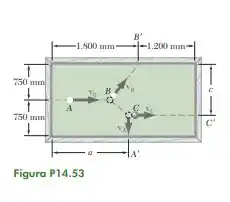
14.53. Em um jogo de bilhar, a bola A tem velocidade inicial v0 ao longo da direção do eixo longitudinal da mesa. Ela atinge a bola B e a seguir a bola C, que estão ambas em repouso. Observa-se que as bolas A e C atingem as laterais da mesa perpendicularmente nos pontos A e C, respectivamente, enquanto a bola B atinge a lateral da mesa obliquamente em B. Sabendo que v0 4 m/s, va 2 m/s e a 1.600 mm, determine (a) as velocidades vB e vC das bolas B e C, (b) o ponto C onde a bola C atinge a lateral da mesa. Considere as superfícies como sendo sem atrito e os choques como perfeitamente elásticos (isto é, conservação de energia).
Passo 1
Já estamos na metade do capítulo, vamos lá!
Para resolver esse problema vamos usar conservação de momento linear.
Para ficar mais organizado ainda, podemos escrever a equação de momento para cada eixo. Para o eixo
Podemos cortar as massas
A gente sabe o valor de , é só olhar o enunciado
Então
Passo 2
E para o eixo
A gente pode cortar as massas
Mas a gente sabe , está no enunciado.
Então
Passo 3
A gente ainda não encontrou a resposta, mas temos mais uma coisa pra usar, a equação da conservação de energia
Para este caso
Podemos cortar
Vamos escrever como
E agora vamos substituir os valores que conhecemos
E aí ficamos com
Passo 4
Esse resultado é essencial para gente, porque com ele conseguimos resolver uma equação que a gente tinha lá no começo, na conservação de momento linear ainda.
Vamos fazer a seguinte alteração
Agora elevamos ao quadrado
Aí fica mais fácil da gente substituir os valores
Agora a gente abre esse quadrado
Então
Aplicando Bhaskaras chegamos em
Finalmente chegamos em uma velocidade para
Passo 5
Agora podemos usar a equação
Para determinar
Vamos substituir os valores
Só falta determinar o ângulo, mas isso não vai ser difícil, a gente tem o módulo de e , isso significa que temos esse triângulo:
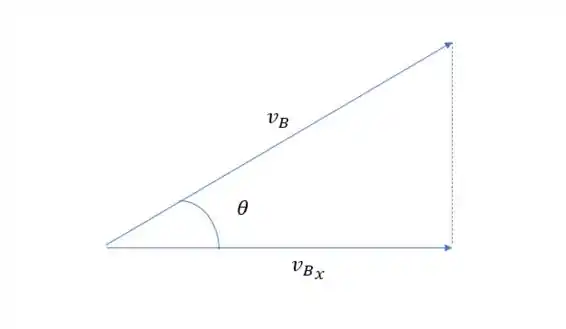
Então a gente pode determinar usando
E isso conclui o item (a)
Passo 6
Mas a questão ainda não acabou, agora vamos para o item (b). Precisamos determinar o ponto C.
Chegou a hora de usar conservação do momento angular.
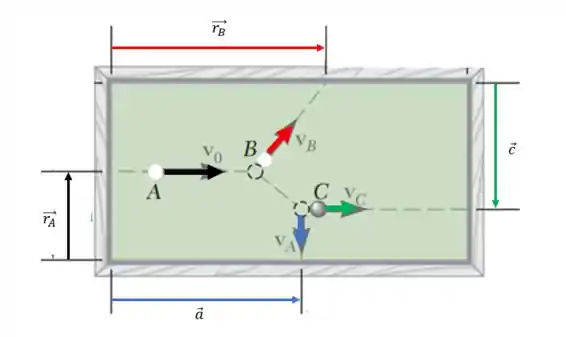
Isso vai ficar
Olha pra imagem. A gente pode ver que a componente em da velocidade está em paralelo com o vetor , então a gente pode desprezar essa componente e reescrever equação assim
Agora todos os vetores velocidades estão perpendiculares aos seus respectivos vetores posição, então a gente pode reescrever a equação assim
Podemos cortar as massas
Passo 7
Agora a gente tem a expressão montada, então vamos substituir os valores que conhecemos, olhando na imagem a gente sabe que
E do enunciado sabemos que
E do item (a) sabemos que
Vamos substituir isso na equação
Isso vai ficar