Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 137

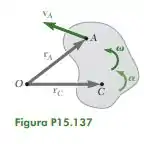
15.137. Representando por rA o vetor de posição do ponto A de uma placa rígida que está em movimento plano, mostre que (a) o vetor de posição rC do centro instantâneo de rotação é

r C = r A + ω × v A ω 2

onde ω é a velocidade angular da placa e vA é a velocidade do ponto A, (b) a aceleração do centro de rotação instantâneo é nula se, e somente se

a A = α ω v A + ω × v A

onde α = α k ^ é a aceleração angular da placa.

Passo 1

Vamos lá! No centro instantâneo de rotação a velocidade é nula, então temos

v C → = 0

A gente consegue calcular a velocidade no ponto A também:

v A → = v C →   + ω → × r A C →

Sendo r A C a distancia entre os pontos A e C.

Então

v A → = ω → ×   r A C →

Passo 2

Vamos pegar a equação e multiplicar por ω →

ω → × v A → = ω → × ω → × r A C →

Isso fica

ω → × v A → = - ω 2 r A C →

Se isolarmos r A C →

r A C → = - ω → × v A → ω 2    

r A C → é um vetor, então podemos inverter seu sentido se invertermos o sinal:

r C A → = ω → × v A → ω 2  

Outra forma que podemos escrever r C A →   é

r C A → = r C → - r A →

Então temos

r C → - r A → = ω → × v A → ω 2  

Logo

r C → = r A → + ω → × v A → ω 2  

E assim respondemos o item (a).

Passo 3

Beleza, agora vamos para o item (b). Temos que mostrar que

a A → = α ω v A → + ω → × v A →

Um modo que temos para calcular a aceleração de forma geral é

a A → = a C → + α → × r A C → + ω → × v A C →

No exercício anterior determinamos

r A C = - ω → × v A → ω 2

E também podemos fazer

v A C → = v A → - v C →

E do enunciado temos

α → = α k ^

E na imagem podemos ver que

α → / / ω →

Logo

ω → = ω   k ^

Então nossa equação fica:

a A → = a C → - α k ^ × ω   k ^ × v A → ω 2 + ω → × v A → - v C →

Podemos simplificar algumas coisas e atribuir v C → = 0 na equação

a A → = a C → - α ω ω 2 k ^ × ( k ^ × v A → ) + ω → × v A →

Então temos

a A → = a C → + α ω v A → + ω → × v A →

Mas como C é o centro instantâneo de rotação

a C → = 0

Logo

a A → = α ω v A → + ω → × v A →

E assim respondemos o item (b).

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra de 100N( ≈ 10k g ) está presa com pino a uma estrutura em movimento em A e é mantida em uma posição vertical por uma corda B C que ode suportar uma tração máxima de 50N sem romper a corda. Qua
Uma barra de 900m m repousa em uma mesa horizontal. A força P aplicada como mostrado na figura produz as seguintes acelerações: a A = 3,6m / s 2 para a direita, α = 6r a d / s 2 no sentido anti-horári
No Problema 15.105, determine o ponto da barra que (a) não tem aceleração, (b) tem uma aceleração de 2,4m / s 2 para a direita.
Uma viga de aço de 5 m está sendo baixada por meio de dois cabos que se desenrolam de guindastes à mesma velocidade. Assim que a viga se aproxima do solo, os operadores dos guindastes aplicam freios p
A aceleração do ponto C é de 0,5 m/s² para baixo e a aceleração angular da viga é de 0,8 rad/s² no sentido anti-horário. Sabendo que, no instante considerado, a velocidade angular da viga é nula, dete