Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 116

No dado instante, o membro AB tem o movimento angular mostrado. Determine a velocidade e a aceleração do bloco deslizante C nesse instante.

Passo 1

Começaremos o exercício encontrando o valor da velocidade linear em B:

v B = ω A B r = 3 0,7 → v B = 2,1   m / s

Passo 2

Agora iremos encontrar o valor da velocidade em C com o auxílio do diagrama a seguir:

v → C = v → B + ω × r → C / B

- v C 4 5 i → - v C 3 5 j → = - 2,1 i → + ω k → × ( - 0,5 i → - 1,2 j → )

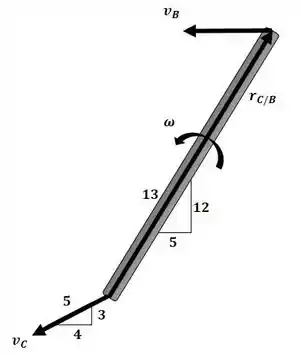
Sendo assim, decompondo nas direções horizontal e vertical:

+ → - 0,8 v C = - 2,1 + 1,2 ω

Essa será nossa equação 1.

+ ↑ - 0,6 v C = - 0 , 5 ω

v C = 0,833 ω

Essa será nossa equação 2. Substituindo essa relação na equação 1:

- 0,8 ( 0,833 ω ) = - 2,1 + 1,2 ω

ω = 1,125   r a d / s

E substituindo esse valor na equação 2:

v C = 0,833 1,125 → v C = 0,938   m / s

Passo 3

Devemos encontrar o valor da aceleração no ponto B:

a B n = ω 2 r = 3 2 0,7 → a B n = 6,3   m / s 2

a B t = α r = 2 0,7 → a B t = 1,4   m / s 2

Agora podemos aplicar a equação da aceleração para o sistema com base no diagrama a seguir:

a → C = a → B + α × r → C / B - ω 2 r → C / B

- a C 4 5 i → - a C 3 5 j → = - 1,4 i → - 6,3 j → + α k → × - 0,5 i → - 1,2 j → - 1,125 2 ( - 0,5 i → - 1,2 j → )

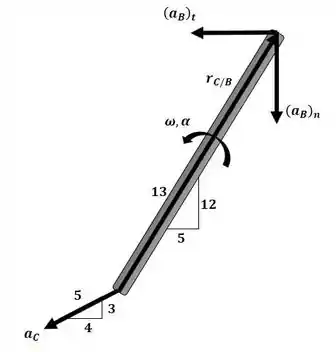
Agora separando nas componentes i e j:

+ → - 0,8 a C = - 1,4 + 1,2 α + 0,6328

α = - 0,666 a C + 0,6393

Essa será nossa equação 3.

+ ↑ - 0,6 a C = - 6,3 - 0,5 α + 1,518

Essa será nossa equação 4. Agora substituindo o a equação 3 na equação 4, temos:

- 0,6 a C = - 6,3 - 0,5 ( - 0,666 a C + 0,6393 ) + 1,518

a C = 5,47   m / s 2

Resposta

v C = 0,938   m / s

a C = 5,47   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O braço A B de 5m de comprimento é usado para fornecer uma plataforma elevada para trabalhadores da construção civil. Na posição mostrada na figura, o braço A B está sendo erguido a uma taxa constante
Um disco com raio de 120m m gira à taxa constante ω 2 = 5r a d / s em relação ao braço A B , que, por sua vez, gira à taxa constante ω 1 = 3r a d / s . Para a posição mostrada na figura, determine a v
Sabendo que, no instante mostrado na figura, a barra AB tem uma velocidade angular constante de 6 rad/s no sentido horário, determine a aceleração do ponto D.
No instante mostrado na figura, a barra AB tem uma aceleração angular nula e uma velocidade angular constante de 8 rad/s no sentido horário. Sabendo que l = 0,3 m, determine a aceleração do ponto médi
Sabendo que, nos instantes mostrados nas figuras, a barra AB tem uma velocidade angular constante de 4 rad/s e uma aceleração angular de 2 rad/s², ambas no sentido horário, determine a aceleração angu