Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 146

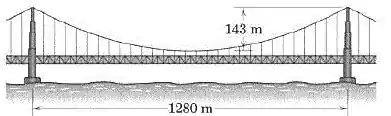
A ponte Golden Gate em São Francisco tem um vão principal de 1280 m, uma deflexão de 143 m e um carregamento estático total de 310,8 kN por metro linear de medida horizontal. O peso de ambos os cabos principais está incluído nesse valor e é considerado uniforme distribuído ao longo da horizontal. O ângulo feito pelo cabo com a horizontal no topo da torre é o mesmo em cada lado de cada torre. Calcule a força trativa no meio do vão em cada um dos cabos principais e a força compressiva C exercida por cada cabo no topo de cada torre.

Passo 1

Primeiro vamos anotar as informações que a questão nos oferece, para facilitar a visualização:

Agora, vamos lembrar que a força trativa no meio do vão é dada pela equação abaixo:

E que, a força compressiva é dada por:

Onde pode ser encontrado por:

Passo 2

Pronto! Anotados as informações e feita as considerações vamos para o cálculo. Mas antes vamos ter cuidado, pois o peso dado na questão é total, mas o peso que a equação da força trativa refere-se é a um lado, dessa maneira:

Com isso, substituindo na equação da força trativa temos:

Passo 3

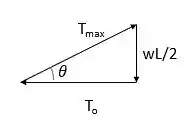
Para acharmos a força compressiva vamos olhar para o triângulo. Note que,

Assim,

Substituindo na equação da força compressiva, teremos:

Portanto:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Expresse F → vetorialmente em termos dos vetores unitários i ^ , j ^ , k ^ . Determine o ângulo entre F → e o eixo y .

A força F → tem um módulo de 900N e atua ao longo da diagonal do paralelepípedo, como mostrado. Expresse F → em termos de seu módulo multiplicado pelo vetor unitário apropriado, e determine seus compo

A torre de transmissão de microondas com 70m de altura é equilibrada por três cabos de amarração, como mostrado. O cabo A B suporta uma força trativa de 12k N . Expresse em forma vetorial a força corr

Expresse F → como um vetor em termos dos vetores unitários i ^ , j ^ e k ^ . Determine a projeção de F → , tanto como um escalar quanto como um vetor, sobre a linha O A , que está situada no plano x -

Expresse a força F → como um vetor em termos dos vetores unitários i ^ , j ^ e k ^ . Determine os ângulos θ x , θ y e θ z que F → faz com os eixos positivos x , y e z .