Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 147
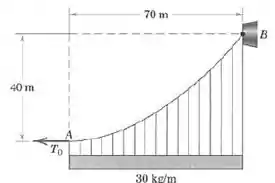
Calcule a força trativa no cabo, em A, necessária para sustentar a carga uniformemente distribuída em relação à horizontal. Determine também o ângulo feito pelo cabo com a horizontal, no ponto de amarração em B.
Passo 1
Primeiro vamos anotar as informações que a questão nos oferece, para facilitar a visualização:
Observe que, o peso é massa vezes a gravidade, ou seja,
Agora, vamos lembrar que a força trativa no cabo é dada pela equação abaixo:
Lembre-se também que:
Passo 2
Pronto! Anotados as informações e feita as considerações vamos para o cálculo, dessa maneira:
Passo 3
Para acharmos o ângulo precisaremos derivar a força trativa, com isso:
E sabemos que:
Logo,
Resposta
Exercícios de Livros Relacionados
Determine a força resultante em A .
Determine as componentes da força que atuam paralela e perpendicularmente ao eixo do poste.
iv)
iii)
O cursor P pode mover-se ao longo da barra OA. Uma corda elástica PC é ligada ao cursor e ao elemento vertical BC. Sabendo que a distância de O até P é 0.15 m e que a tração na corda é 13 N, determine