Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 18.Problemas - Ex. 64

18.64. Determine a taxa de variação G da quantidade de movimento angular HG do disco do Problema 18.4, admitindo que, no instante considerado, o conjunto tenha uma velocidade angular j e uma aceleração angular α j.

Passo 1

Beleza vamos para mais uma questão. No problema 18.4 temos um disco homogêneo de massa m e raio r está montado em um eixo vertical AB, com a normal formando um ângulo β = 25 ° , com o eixo. A velocidade do eixo é constante igual a ω .

Para esse problema vamos precisar usar os eixos principais G x ' y ' z ' .

E

z ' = z

Passo 2

O próximo passo é calcular os momentos de inércia:

I x ' = 1 4 m r 2 + 1 12 m L 2

Sendo L a espessura do disco, mas para esse problema podemos desprezar essa espessura, então

I x ' = 1 4 m r 2

Analogamente

I z ' = 1 4 m r 2

E por último

I y ' = 1 2 m r 2

E vamos converter a velocidade angular para os novos eixos:

ω x ' = - ω ⋅ sin ⁡ β ω y ' = ω ⋅ cos ⁡ β ω z ' = 0

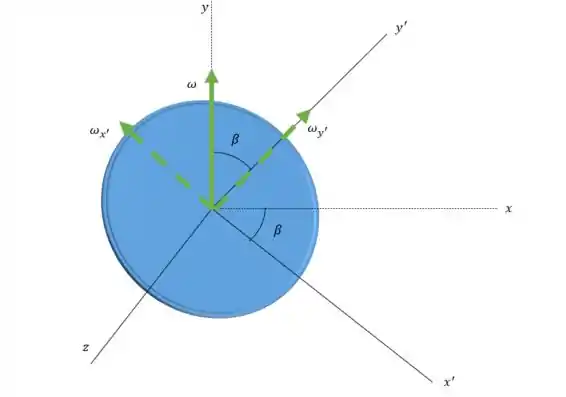
Passo 3

Agora temos tudo para calcular o momento angular em torno do ponto G.

H G = H x '   i ^ ' + H y '   j ^ ' + H z ' k ^ '

Isso fica

H G = I x ' ω x '   i ^ ' + ( I y ' ω y ' )   j ^ ' + I z ' ω z ' k ^ '

Substituindo os valores dos momentos inércia e velocidade angular:

H G = 1 4 m r 2 ⋅ - ω ⋅ sin ⁡ β   i ^ ' + 1 2 m r 2 ⋅ ω ⋅ cos ⁡ β   j ^ ' + 1 4 m r 2 ⋅ 0 k ^ '

Ou seja

H G = - 1 4 m r 2 ω sin ⁡ β i ^ ' + 1 2 m r 2 cos ⁡ β   j ^ '

Passo 4

Nesse problema nós estamos assumindo que existe uma aceleração angular α = α   j ^ , olha lá no enunciado.

A aceleração angular é a derivada da velocidade angular, então sabemos que:

α   j ^ = ω ˙ x ' ,     ω ˙ y ' , ω z '  

Ou seja

α   j ^ = ( - α sin ⁡ β ,   α cos ⁡ β ,   0 )

E como nós mudamos nosso referencial rotacional, vamos fazer:

Ω = ω   j ^ = - ω sin ⁡ β i ^ + ( ω cos ⁡ β )   j ^

Passo 5

Agora vamos calcular a variação do momento angular no referencial G x ' y ' z '

H ˙ G G x ' y ' z ' = I x ' ω ˙ x '   i ^ ' + I y ' ω ˙ y '   j ^ ' + I z ' ω ˙ z '   k ^ '

Substituindo os valores

= 1 4 m r 2 ⋅ - α ⋅ sin ⁡ β   i ^ ' + 1 2 m r 2 ⋅ α ⋅ cos ⁡ β   j ^ ' + 1 4 m r 2 ⋅ 0 k ^ '

Isso fica

= - 1 4 m r 2 α sin ⁡ β i ^ ' + 1 2 m r 2 α cos ⁡ β   j ^ '

Agora vamos converter isso para os eixos cartesianos:

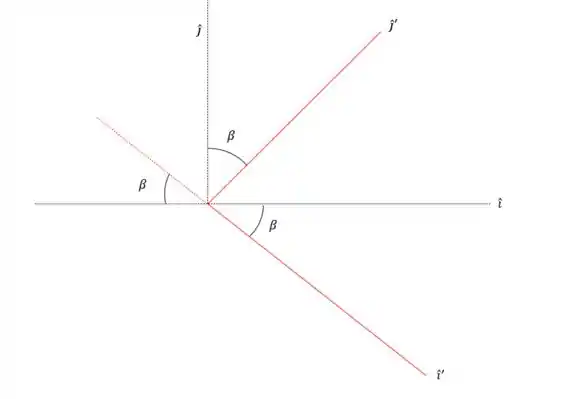
Olha só para a imagem, nós podemos dizer que:

i ^ ' = cos ⁡ β   i ^ - sin ⁡ β   j ^

E

j ^ ' = sin ⁡ β   i ^ + c o s   β   j ^

Então para convertemos para os eixos cartesianos basta fazer

= - 1 4 m r 2 α sin ⁡ β i ^ ' + 1 2 m r 2 α cos ⁡ β   j ^ '

= - 1 4 m r 2 α sin ⁡ β cos ⁡ β   i ^ - sin ⁡ β   j ^ + 1 2 m r 2 α cos ⁡ β   sin ⁡ β   i ^ + c o s   β   j ^

Isso fica

= - 1 4 m r 2 α sin ⁡ β cos ⁡ β + 1 2 m r 2 α cos ⁡ β sin ⁡ β i ^ + 1 4 m r 2 α sin 2 ⁡ β + 1 2 m r 2 α cos 2 ⁡ β j ^

Simplificando

H ˙ G G x ' y ' z ' = 1 4 m r 2 α sin ⁡ β cos ⁡ β i ^ + 3 4 m r 2 α sin 2 ⁡ β + cos 2 ⁡ β j ^

Finalmente a equação diminui um pouco!

Passo 6

Agora vamos calcular a mesma coisa, mas no referencial fixado G x y z

H ˙ G = H ˙ G G x ' y ' z ' + Ω × H G

Vamos primeiro resolver Ω × H G para não ficar uma equação gigante.

Ω × H G = [ - ω sin ⁡ β i ^ + ω cos ⁡ β )   j ^ × - 1 4 m r 2 ω sin ⁡ β i ^ ' + 1 2 m r 2 cos ⁡ β   j ^ '

Isso fica

= 1 4 m r 2 ω 2 cos ⁡ β sin ⁡ β   k ^ + - 1 2 m r 2 ω 2 sin ⁡ β cos ⁡ β k ^

= - 1 4 m r 2 ω 2 sin ⁡ β cos ⁡ β k ^

Agora vamos somar com H ˙ G G x ' y ' z '

H ˙ G = 1 4 m r 2 α sin ⁡ β cos ⁡ β i ^ + 3 4 m r 2 α sin 2 ⁡ β + cos 2 ⁡ β j ^ + - 1 4 m r 2 ω 2 sin ⁡ β cos ⁡ β k ^

Podemos colocar m r 2 em evidencia.

H ˙ G = m r 2 1 4 α sin ⁡ β cos ⁡ β i ^ + 3 4 α sin 2 ⁡ β + cos 2 ⁡ β j ^ - 1 4 ω 2 sin ⁡ β cos ⁡ β k ^

Beleza, chegamos em uma equação para H ˙ G , estamos quase acabando, só falta substituir o valor de β agora.

H ˙ G = m r 2 1 4 α sin ⁡ 25 ° cos ⁡ 25 ° i ^ + 3 4 α sin 2 ⁡ 25 ° + cos 2 ⁡ 25 ° j ^ - 1 4 ω 2 sin ⁡ 25 ° cos ⁡ 25 ° k ^

Fazendo todas essas contas temos

H ˙ G = m r 2 0,0958   α i ^ + 0,455   α j ^ - 0,0958   ω 2 k ^

E acabamos mais um!

Resposta

H ˙ G = m r 2 0,0958   α i ^ + 0,455   α j ^ - 0,0958   ω 2 k ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A haste AB de 4 kg está presa a um colar de massa desprezível em A e a um volante em B. O volante tem massa de 16 kg e raio de rotação de 180 mm. Sabendo-se que na posição mostrada a velocidade angula
O motor mostrado gira a uma frequência de 22,5 Hz e opera uma máquina ligada ao eixo em B. Sabendo que o motor desenvolve 3 kW, determine a magnitude do acoplamento exercido (a) pelo motor na polia A,
Se no Problema 17.45 a velocidade angular do volante deve ser a mesma na posição mostrada e quando o Ponto B está diretamente acima de G, determine o valor requerido de sua velocidade angular na posiç
As barras uniformes AB e BC pesam 2,4 lb e 4 lb, respectivamente, e a roda pequena em C tem peso desprezível. Sabendo que na posição mostrada a velocidade da roda C é 6 ft/s para a direita, determine
A engrenagem de raio de 80 mm mostrada tem uma massa de 5 kg e um raio de giração centróide de 60 mm. A haste de 4 kg AB é presa ao centro da engrenagem e a um pino em B que desliza livremente em uma