Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 8

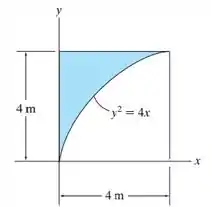
Determine a área e o centroide (overset(-)(x) , overset(-)(y)) da área.

Passo 1

Vamos começar enxergando nosso elemento diferencial, ele é a área em cinza na figura:

Essa área é dada por:

d A = x ⅆ y

Vamos usar nossa função em função de y , ficando x = y^2 // 4 , assim:

d A = (y^2)/(4) ⅆ y

O centroide do nosso elemento diferencial é dado por:

overset(-)(x) = (x)/(2)

Substituindo nossa função ficamos com:

overset(-)(x) = ((y^2 // 4))/(2) = (y^2)/(8)

Enquanto que para nosso overset(-)(y) vai ser justamente overset(-)(y) = y .

Passo 2

Para nossa área teremos:

A = int_A ⅆ A

A = x ⅆ y = int_0^4 (y^2)/(4) ⅆ y = ((y^3)/(12)|_0^(4 m) = 5,33 m^2

Passo 3

Vamos agora encontrar nosso centroide.

Para overset(-)(x) teremos:

overset(-)(x) = (int_A overset(-)(x) ⅆ A)/(int_A ⅆ A)

overset(-)(x) = (int_0^(4 m) (y^2)/(8) ((y^2)/(4) d y))/(5,33) = (int_0^(4 m) (y^4)/(32) ⅆ y)/(5,33) = ((((y^5)/(160))|_0^(4 m))/(5,33) = 1,2 m

E para overset(-)(y) teremos:

overset(-)(y) = (int_A y ⅆ A)/(int_A ⅆ A)

overset(-)(y) = (int_0^(4 m) y ((y^2)/(4) ⅆ y))/(5,33) = (int_(Theta)^(4 m) ((y^3)/(4)) ⅆ y)/(5,33) = ((((y^4)/(16))|_0^(4 m))/(5,33) = 3 m

Resposta

A = 5,33 m^2

overset(-)(x) = 1,2 m

overset(-)(y) = 3 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área e o centroide x - , y - da área.
Determine a área o centroide ( x - ,y - ) da área.
Determine a massa e localize o centro de massa ( x - ,y - ) da barra uniforme. A massa por unidade de comprimento da barra é 3 kg/m.
Determine a localização ( x - , y - ) do centroide do fio.
Localize o centroide x - da área sombreada.