Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 131

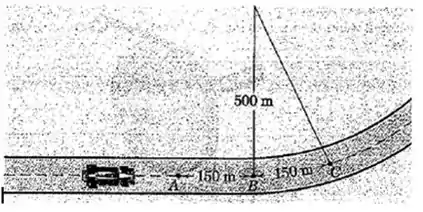
2/131) Um piloto decorridas guiando a uma velocidade de 250 k m / h no trecho de pista reta aplica os freios no ponto A e reduz sua velocidade a uma taxa uniforme para 200 k m / h em C em uma distância de 150 + 150 = 300 m . Calcule o módulo da aceleração total do carro de corrida um instante após este passar no ponto B .

Passo 1

Então galera, como a aceleração tangencial é constante entre os pontos A e C , podemos usar a equação de torricelli para calcularmos o seu valor :

v c 2 = v A + 2 a t ∆ s A - C  

Como sabemos que v A = 250 3,6 m / s e v C = 200 3,6 m / s , temos que :

a t = 200 2 - 250 2 3,6 2 2 300 = - 2,89   m / s 2

Passo 2

De forma análoga ao passo anterior, como a aceleração tangencial é constante entre os pontos A e B , podemos usar a equação de torricelli para calcularmos o valor da velocidade em B :

v B 2 = v A 2 + 2 a t ∆ s A - B

v B 2 = 250 3,6 2 + 2 - 2,89 150 = 3954 m s 2

v B = 62,9 m s

Passo 3

Agora que conhecemos a velocidade no ponto B , podemos calcular o valor da acelração normal neste ponto através da fórmula:

a n = v B 2 ρ

a n = 3954 500 = 7,91 m s 2

Com isso , para acharmos aceleração total em B , basta aplicarmos a fórmula :

a = a n 2 + a t 2 = 7,91 2 + 2,89 2 = 8,42   m / s 2

Resposta

a = 8,42   m / s 2

Suave pessoal? Então partiu fazer mais exercícios como esse!!!!!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O movimento do pino P é restringido pela fenda curva da lemniscata em O B e pela fenda do braço O A . Se O A gira no sentido anti-horário com uma velocidade angular de θ ˙ = 3r a d / s , determine a i
O movimento do pino P é restringido pela fenda curva da lemniscata em O B e pela fenda do braço O A . Se O A gira no sentido anti-horário com uma velocidade angular de θ ˙ = 3 t 3 / 2r a d / s , onde
O motorista do carro mantém uma velocidade escalar constante de 40 m / s . Determine a velocidade angular da câmera acompanhando o carro quando θ = 15 ° .
A caixa desce deslizando pela rampa helicoidal com uma velocidade escalar constante de v = 2m / s . Determine a intensidade da sua aceleração. A rampa desce uma distância vertical de 1m para cada volt
O pino move-se na fenda curva definida pela lemniscata e pela fenda no braço. Em θ = 30 ° , a velocidade angular é θ ˙ = 2r a d / s , e a aceleração angular é θ ¨ = 1,5r a d / s 2 . Determine as inten