Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 152

2/152) A guia horizontal fixa suporta um cursos e um pino P cujo movimento é controlado pelo braço ranhurado rotativo OA . Se o braço está girando em torno de O a uma taxa constante de θ ' = 2 r a d / s para um intervalo do seu movimento projetado , determine os módulos da velocidade e da aceleração do cursor na ranhura para o instante em que θ = 60 ° . Encontre também as componentes r da velocidade e da aceleração .

Passo 1

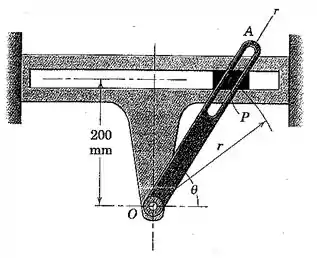
Então pessoal , analisando a figura do problema obtemos que :

h = x tan ⁡ θ

0 = x ' . tan ⁡ θ + x θ ' . sec 2 ⁡ θ

x ' . tan ⁡ θ + h   c t n   θ θ ' . sec 2 ⁡ θ = 0

O módulos da velocidade e sua componente r podem ser obtidos pelas relações :

v = - x ' = h θ ' c o t n sec 2 ⁡ θ tan ⁡ θ

v = h θ ' csc 2 ⁡ θ

v = 200 2 2 3 2 = 533 m m / s  

v r = - v cos ⁡ θ

v r = - 533 1 2 = - 267   m m / s

Passo 2

Além disso , nós sabemosque :

- a = v ' = ( h θ ' csc 2 ⁡ θ ) '

v ' = h θ ' ' c os s e c ⁡ θ - c o t n θ c os s e c ⁡ θ θ '

- a = - 2 h θ ' ' c o t n θ c o s se c 2 ⁡ θ

O modulo da aceleração e a sua component r podem ser calculados respectivamente por :

a = 2 200 2 2 1 3 2 3 2 = 1232   m m / s 2

a r = a cos ⁡ θ = 1232 1 2 = 616   m m / s 2

Resposta

v = 533 m m / s  

v r = - 267   m m / s

a = 1232   m m / s 2

a r = 616   m m / s 2

Tranquilo pessoal? Bora resolver mais questões então

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula P se desloca na trajetória circular mostrada. Desenhe o vetor aceleração a e determine o seu módulo a para os seguintes casos:(a) a velocidade v é 1,2m / s e é constante,(b) a velocidade
2/165) Para as condições do Prob. 2/164 , determine θ ' como uma função do tempo .
O foguete lançado verticalmente e o radar de rastreamento do Prob. 2/147 são apresentados aqui novamente. No instante em que θ = 60 ° , as medidas fornecem θ ˙ = 0,03r a d / s e r = 7500m , e a aceler
O deslocamento angular da centrífuga é dado por θ = 4 t + 30 e - 0,03 t - 30r a d , onde t é expresso em segundos e t = 0 é o instante da partida. Se o ser humano perde a consciência em um nível de ac
2/168) Uma cápsula P de fogos de artifício lançada em uma trajetóra vertical tem uma aceleração y dada por a y = - g - k v 2 , onde o último termo é devido ao arrasto aerodinâmico . Se a velocidade da