Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 57

Para os cabos do Problema 2.45, sabe-se que a máxima tensão admissível é de 600 N no cabo AC e 750 N no cabo BC. Determine a máxima força que pode ser aplicada em C, o correspondete valor de .

Passo 1

Tá legal, vamos lá! Antes de começar o exercício, é sempre bom ter em mente as dicas que o próprio livro nos dá antes de cada seção de exercícios, na parte de “metodologia para resolução de problemas”. Então beleza, seguindo aquelas dicas, vamos começar fazendo o diagrama de corpo livre:

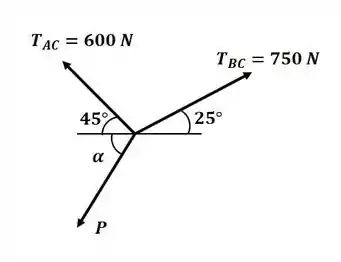
Passo 2

Agora que temos o DCL do problema, e temos somente três forças, vamos desenhar o triângulo de forças do sistema para descobrir os valores das tensões:

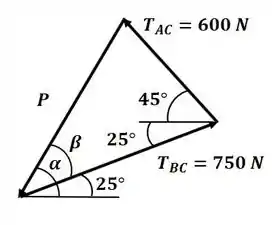
Nesse caso, precisamos do valor de para depois encontrar o valor de , então vamos aplicar a lei dos cossenos para descobrir :

Passo 3

Agora só precisamos aplicar a lei dos senos para esse triângulo, que será:

Isolando e resolvendo:

E, do triângulo de forças do passo 2, temos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.29. A massa de 700k g é suspensa por um gancho que se move ao longo de um trilho d = 1,7m até d = 3,5m . Determine a força ao longo da cantoneira conectada por pino BC (ligação curta) e a intensidad

5.39. A mola CD permanece na posição horizontal o tempo todo devido ao rodízio em D. Se a mola está descarregada quando θ = 0 e a rigidez é k = 1,5 k N m , determine o menor ângulo θ para o equilíbrio

5.52. Três livros uniformes, cada um com peso W e comprimento a , são empilhados como na figura. Determine a distância máxima d que o livro do topo pode se projetar em relação ao da base, de modo que

5.43. A barra uniforme AB possui peso de 75N . Determine a força no cabo quando a barra está na posição mostrada.

5.53. Determine o ângulo θ em que a ligação ABC se mantém em equilíbrio se o membro BD se mover 50m m para a direita. As molas estão originalmente descarregadas quando θ = 0 ° . Cada mola possui a rig