Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 24
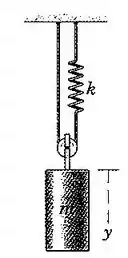
24. O cilindro de massa recebe um deslocamento vertical a partir de sua posição de equilíbrio e é solto. Escreva a equação diferencial para a vibração vertical do cilindro e determine o período do seu movimento. Despreze o atrito e a massa da polia.
Passo 1
Bom, primeiro a gente vai montar o diagrama de corpo livre no bloco e na polia
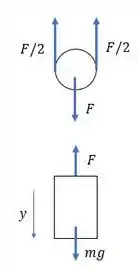
Passo 2
Quando o deslocamento foi zero, teremos:
Já para um deslocamento de sendo , a mola estará alongada por . Então:
Passo 3
Agora faremos o somatório de forças no eixo :
Onde é a aceleração em .
Rearranjando a expressão:
Sabemos que a equação genérica para um movimento harmônico:
Portanto:
E sabemos também que:
Substituindo os valores para encontrar :
Passo 4
Agora, vamos calcular o período pela fórmula:
Resposta
O período de oscilação será:
Exercícios de Livros Relacionados
46. Desenvolva a equação do movimento em termos da variável x para o sistema apresentado. Determine uma expressão para o fator de amortecimento ζ em termos das propriedades conhecidas do sistema. Desp
22. O grande recipiente de cimento, suspenso pelo guindaste por um cabo elástico, possui uma massa de 4000k g . Quando o recipiente é perturbado, uma oscilação vertical com período de 0,5s é observada
28. Determine o valor do fator de amortecimento ζ para o sistema massa-mola-amortecedor simples apresentado.
21. Uma pequena partícula de massa m está presa a dois fios muitos tensos, conforme mostrado. Determine a frequência natural ω n do sistema para pequenas oscilações verticais se a tração T em ambos os