Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 22
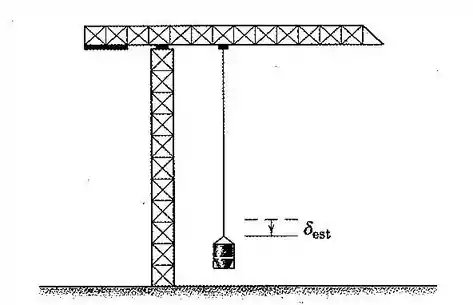
22. O grande recipiente de cimento, suspenso pelo guindaste por um cabo elástico, possui uma massa de . Quando o recipiente é perturbado, uma oscilação vertical com período de é observada. Qual é o deslocamento estático do balde? Despreze a massa do cabo e considere que o guindaste é rígido para a posição de sustentação mostrada.
Passo 1
Bom, primeiro a gente vai montar a fórmula do período de oscilação :
Onde é a frequência angular. Mas se a gente lembrar que:
Temos:
Substituindo os valores:
Passo 2
Agora faremos o somatório de forças no eixo :
A soma é zero, pois queremos o equlíbrio.
Onde é o deslocamento que foi pedido.
Substituindo os valores:
Resposta
O deslocamento estático do balde será:
Exercícios de Livros Relacionados
37. Um sistema massa-mola amortecido é liberado a partir do repouso com deslocamento inicial positivo x 0 . Se o deslocamento máximo positivo seguinte é x 0 / 2 , determine o fator de amortecimento ξ
36. Para o sistema massa-mola amortecido mostrado, determine o coeficiente de amortecimento viscoso para o qual ocorrerá um amortecimento crítico
39. Um aperfeiçoamento posterior do projeto para a plataforma de pesagem do problema 8.14 é apresentado aqui, onde dois amortecedores viscosos foram adicionados para limitar a razão de sucessivas ampl
38. Se a amplitude do oitavo ciclo de um oscilador linear com amortecimento viscoso é dezesseis vezes a amplitude do vigésimo ciclo, calcule o fator de amortecimento ξ .
44. O proprietário de uma caminhonete de 1660k g testa a ação dos amortecedores traseiros aplicando uma força constante de 450N ao para-choque traseiro e medindo um deslocamento estático de 75m m . Ap