Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 46
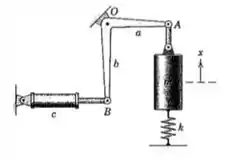
46. Desenvolva a equação do movimento em termos da variável para o sistema apresentado. Determine uma expressão para o fator de amortecimento em termos das propriedades conhecidas do sistema. Despreze a massa da barra curva e assuma pequenas oscilações em torno da posição de equilíbrio mostrada.
Passo 1
Bom, primeiro a gente vai montar um diagrama de forças para o sistema:
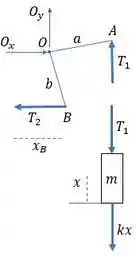
Aqui, teremos a seguinte relação:
E se derivarmos em relação ao tempo uma vez:
E temos também que a força é a força que atua no amortecedor, então:
Passo 2
Calcularemos o somatório de momentos em relação ao ponto :
Substituindo :
Passo 3
Agora, faremos o somatório de forças no eixo para cada massa:
Onde é a aceleração
Aqui, é a constante da mola. Substituindo :
Rearranjando a equação:
Passo 4
Agora, vamos calcular o fator de amortecimento Pela equação:
Onde é a constante do amortecedor e é a frequência natural do sistema.
Mas não temos a frequência , não é? Então, devemos usar a relação:
Porém, como sabemos a equação genérica para um movimento harmônico amortecido:
Então:
Resposta
A equação diferencial de movimento do sistema é:
E o fator de amortecimento será: