Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 21

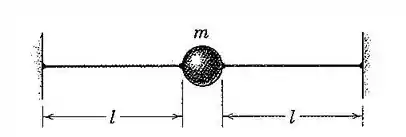
21. Uma pequena partícula de massa m está presa a dois fios muitos tensos, conforme mostrado. Determine a frequência natural ω n do sistema para pequenas oscilações verticais se a tração T em ambos os fios é considerada constante. O cálculo do pequeno deslocamento estático da partícula é necessário?

Passo 1

Bom, primeiro a gente vai montar o diagrama de corpo livre da massa m com um certo desocamento de ângulo θ :

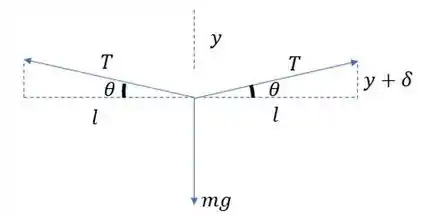
Aqui, y será a deflexão dinâmica do sistema, ou seja, a deflexão que ocorre devido à vribração e δ será a deflexão est´taica, ou seja, devido à força peso.

Para ângulos pequenos s e n ( θ ) ≅ θ e por estar em radianos e plea definição de radianos de arco dividido pela raio, temos:

θ ≅ y + δ l

Passo 2

Agora faremos o somatório de forças no eixo y :

∑ F y = m y ¨

Onde y ¨ é a aceleração.

- 2 T ⋅ s e n θ + m g = m y ¨

- 2 T ⋅ y + δ l + m g = m y ¨

- 2 T y l - 2 T δ l + m g = m y ¨

Porém, as forças - 2 T δ l e m g tem mesma intensidade, e a soma das duas da zero. Então:

- 2 T y l = m y ¨

Rearranjando a equação:

y ¨ + 2 T l m y = 0

Passo 3

Sabemos que a equação genérica de movimento harmônico é:

y ¨ + ω n 2 y = 0

Disso, tiramos que:

ω n 2 = 2 T l m

∴ ω n = 2 T l m     ( r a d / s )

Passo 4

Como fizemos ali em cima adicionamos as forças do cálculo de deslocamento estático da partícula e sua soma resultou em zero, portanto não é necessário calculá-lo.

Resposta

A frequência natural do sistema para pequenas vibrações será:

ω n = 2 T l m     ( r a d / s )

E o cálculo do deslocamento estático não é necessário.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

20. Um para-choque de um automóvel que absorve energia, com suas molas inicialmente sem deformação, possui uma constante de mola equivalente de 535k N / m . Se o carro de 1200k g se aproxima de uma pa
23. A boia cilíndrica flutua em água salgada (massa específica de 1030k g / m 3 ) e possui uma massa de 800k g , com um centro de massa baixo para mantê-la estável na posição vertical. Determine a fre
19. Calcule a frequência natural ω n do sistema mostrado na figura. A massa e o atrito das polias são desprezíveis.
45. Desenvolva a equação diferencial do movimento para o sistema mostrado em sua posição de equilíbrio. Despreze a massa do elemento de ligação A B e admita pequenas oscilações.
26. Desenvolva a equação diferencial do movimento para o sistema mostrado, em termos da variável x 1 . A massa do mecanismo é desprezível. Determine a frequência natural ω n ' em r a d / s para o caso