Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 20

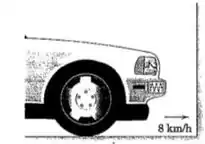
20. Um para-choque de um automóvel que absorve energia, com suas molas inicialmente sem deformação, possui uma constante de mola equivalente de 535   k N / m   . Se o carro de 1200   k g se aproxima de uma parede de grande massa com uma velocidade de 8   k m / h , determine

(a) a velocidade v do carro como uma função do tempo durante o contato com a parede, onde t = 0 é o instante de início do impacto, e

(b) a deflexão máxima x m á x do para-choque.

Passo 1

Bom, primeiro a gente vai montar o diagrama de corpo livre de um sistema massa-mola equivalente ao choque:

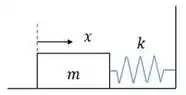
Passo 2

Agora, Calcular a frequência natural do sistema ω n pela fórmula:

ω n = k m

Onde k é a constante de mola e m a massa do carro

ω n = 525000   N / m 1200   k g

ω n = 437,5

ω n ≅ 20,92   r a d / s

Passo 3

Montaremos a equação que descreve o movimento da massa no sistema massa-mola equivalente:

x = x 0 ⋅ cos ⁡ ω n t + x ˙ 0 ω n s e n ( ω n t )

Aqui, x 0 vale zero e x ˙ 0 é a velocidade dada. Porém, ela está em k m / h e precisamos dela em m / s , então dividiremos por 3,6 :

v = 8   k m / h 3,6 = 2,22   m / s

Isso nos da:

x = 0 + 2,22 m s 20,92 r a d s ⋅ s e n ( 20,92 r a d s ⋅ t )

∴ x = 0,106 ⋅ s e n ( 20,92 t )

Passo 4

(a) Para achar a função da velocidade, vamos derivar a equação de x encontrada:

v = x ˙ = d d t x

d d t x = d d t 0,106 ⋅ s e n ( 20,92 t )

x ˙ = 0,106 ⋅ cos ⁡ 20,92 t ⋅ 20,92   m / s

∴ x ˙ = 2,22 ⋅ cos ⁡ 20,92 t m / s

Passo 5

(b) Para a deflexão máxima x m á x , devemos encontrar o maior valor para x na equação:

x = 0,106 ⋅ s e n ( 20,92 t )

O qual é dado quando s e n ϕ = 1

∴ x = 0,106   m

Resposta

(a) A equação de velocidade do sistema será:

x ˙ = 2,22 ⋅ cos ⁡ 20,92 t m / s

(b) E a deflexão máxima x m á x :

x = 0,106   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

18. Com a hipótese de deslizamento, determine a massa m do bloco, que deve ser colocado em cima do carrinho de 6k g a fim de que o período do sistema seja de 0,75s . Qual é o coeficiente de atrito est
A placa triangular uniforme gira livremente em torno de um eixo horizontal que atravessa o ponto O . Determine a frequência natural para pequenas oscilações.
Uma viga I com 20 m está sendo erguida pelo esquema de cabos mostrado. Determine o período τ das pequenas oscilações em torno da conexão O , que se supõe permanecer fixa e em torno da qual os cabos gi
O disco circular uniforme está suspenso por uma cavidade (não mostrada) que se encaixa sobre a pequena esfera de fixação em O . Determine o período para movimentos pequenos, se o disco oscila livremen
140. A massa de 4k g está suspensa pela mola de rigidez k = 350N / m e está inicialmente em repouso na posição de equilíbrio. Se uma força para baixo F = C t é aplicada ao corpo e atinge um valor de 4