Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 5

O pêndulo da máquina de impacto Charpy com massa de 50 kg e raio de giração ka=1,75m é solto quando θ=0°. Determinar sua velocidade angular logo antes de atingir o corpo de prova S, onde θ=90°.

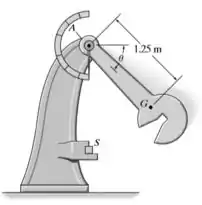
Passo 1

Analisando as reações ocorrendo no sistema, temos:

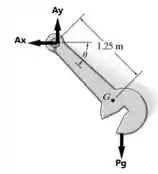
Sabemos que a soma das energias no instante 1, quando θ=0° será igual a soma das energias no instante 2 quando θ=90°. Logo:

T t o t a l 1 + ∑ U 1 - 2 = T t o t a l 2

Porém, sabendo que o pêndulo parte do repouso e que a energia no estágio 2 será puramente a energia cinética do pêndulo, temos:

0 + ∑ U 1 - 2 = T a

Logo,

∑ U 1 - 2 = T a

Passo 2

Sabendo que ∑U1-2 será dado, neste caso, pela multiplicação do seu peso pela distância ao ponto A, e sabendo que:

T a = 1 2 × m × k a ² × ω ²

Logo teremos que:

50 × 9,81 × 1,25 = 1 2 × m × k a ² × ω ²

Como temos kg=325mm e mg=200Kg, teremos:

50 × 9,81 × 1,25 = 1 2 × 50 × 1,75 ² × ω ²

Isolando ω, temos:

ω = 50 × 9,81 × 1,25 × 2 50 × 1,75 ² = 2,83 r a d / s

Resposta

A velocidade angular do pêndulo solto do repouso, quando chega em θ=90° será de 2,83rad/s.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A bobina tem uma massa de 60k g e raio de giração k G = 0,3m . Se ela é liberada do repouso, determine a que distância seu centro desce pelo plano liso, antes de atingir uma velocidade angular de ω =
O tambor tem massa de 50k g e raio de giração em relação ao pino em O , k O = 0,23m . Se o bloco de 15k g desloca-se para baixo a 3m / s , e uma força P = 100N é aplicada à alavanca do freio, determin
Um homem com massa de 90k g está sentado em uma cadeira da roda-gigante, a qual, excluindo-se o homem tem massa de 7500k g e raio de giração k O = 11,1m . Se um torque M = 120 10 3N ⋅ m é aplicado em
Um homem com massa de 75k g está agachado na extremidade do trampolim, como mostra a figura. Nessa posição, o raio de giração em relação a seu centro de gravidade é k G = 0,36m . Enquanto mantém sua p
A bobina tem massa de 75k g e raio de giração k O = 0,675m . Se uma corda é enrolada em torno de seu miolo interno e sua extremidade é puxada com uma força horizontal P = 200N , determine a velocidade