Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 6

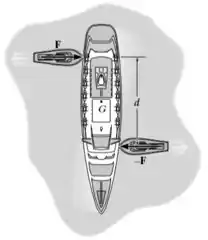
Os dois rebocadores exercem uma força de intensidade F cada uma, sobre o navio de massa m e raio de giração kg, que estão sempre direcionadas perpendicularmente a linha central do navio. Determinar sua velocidade angular após ele girar 90° e sabendo que está inicialmente em repouso.

Passo 1

Analisando as reações ocorrendo no sistema, sabemos que os rebocadores exercem um momento sobre o ponto G indicado na figura, que se dá por:

M = F × d

Temos que o momento de inércia de massa do navio será dado por:

I g = m × k g 2 × ω ²

Sabemos que a soma das energias no instante 1, quando θ=0° será igual a soma das energias no instante 2 quando θ=90°. Logo:

T t o t a l 1 + ∑ U 1 - 2 = T t o t a l 2

Porém, sabendo que o navio está inicialmente em repouso, temos:

0 + ∑ U 1 - 2 = T t o t a l 2

Sabendo que no estágio 1, a energia total será dada epenas pela multiplicação do momento gerado pelos empurradores com o ângulo deslocado, e que, no estágio 2, a energia cinética estará relacionada apenas com o momento de inercia de massa do navio e sua velocidade angular, temos:

M × θ = 1 2 × I g × ω ²

Passo 2

Como foi dado que o navio rotacionou 90°, temos que θ=90°=π/2 rad.

Aplicando na equação obtida, temos:

M × π 2 = 1 2 × I g × ω ²

Tendo que M=F*d e que Ig=m*kg², temos:

F × d × π 2 = 1 2 × ( m × k g 2 ) × ω ²

Isolando ω, temos:

ω = F × d × π m × k g 2

Rearranjando, temos:

ω = 1 k g × F × d × π m

Resposta

A velocidade angular do navio, que parte do repouso, de θ=0° e, quando chega em θ=90° será dada pela expressão:

ω = 1 k g × F × d × π m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

163. Cada uma das barras uniformes O A e O B possui uma massa de 2k g e é articulada livremente em O ao eixo vertical, que recebe uma aceleração constante a = g / 2 . As hastes que conectam o cursor l
O tacômetro mecânico mede a velocidade de rotação N do eixo pelo movimento horizontal do cursor B ao longo do eixo que gira. Esse movimento é causado pela ação centrífuga das duas massas A de 350 g, q
A plataforma móvel de trabalho é elevada por meio de dois cilindros hidráulicos articulados nos pontos C. A pressão em cada cilindro produz uma força F. A plataforma, o homem e a carga têm uma massa c
Cada um dos três painéis idênticos uniformes de uma porta industrial segmentada tem massa m e é conduzido nos trilhos (um mostrado em linha tracejada). Determine a aceleração horizontal a do no painel
O setor e as rodas vinculadas são liberados a partir do repouso na posição mostrada no plano vertical. Cada roda é um disco circular maciço com uma massa 5 k g e rola sobre a trajetória circular fixa