Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 3
Uma força de 20N é aplicada ao cabo que faz a bobina de raio de giração rg=0,42m e massa de 175kg girar sobre os rolos A e B, sem deslizar. Determinar sua velocidade angular ao completar duas revoluções, saindo do repouso. Os rolos podem ser considerados cilindros de raio de 0,1m e a massa do cabo pode ser desprezada.
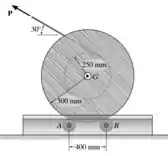
Passo 1
Analisando as reações ocorrendo no sistema, temos:
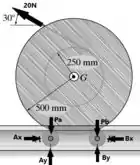
Onde Pa e Pb são os pesos dos rolos A e B, respectivamente. Temos que pela lei da conservação de energia, a soma de todas energias presentes no sistema no início, será igual a soma de suas energias no final, como o sistema sai do repouso no instante 1, e depois passa a ter movimento até o estágio 2, onde terá apenas energia cinética, temos:
Assim, sabendo que no estágio 1 o sistema está em repouso, temos:
Logo,
Passo 2
Tendo isso, podemos organizar a equação como:
Onde rp é o raio formado pela linha de ação da força e o centro G da bobina, Tg, Ta e Tb são as energias cinéticas da bobina, e dos rolos A e B, respectivamente. Porém, como os rolos possuem simetria, e neste caso, pelas condições, suas energias cinéticas serão iguais, logo:
Ou
Para a energia cinética da bobina, temos:
Para os rolos, temos:
Logo teremos:
Substituindo os valores, temos:
Assim, temos:
Passo 3
Porém, sabemos que na interface entre a bobina e os rolos temos a mesma velocidade tangencial, temos que:
Portanto
substituindo o valor de ωa em (1), temos:
Com isso, temos:
Resposta
A velocidade angular da bubina será de 1,78rad/s, após 2 revoluções em torno de seu centro G. E isso também implica que a velocidade angular dos rolos será 5 vezes maior, como já vimos anteriormente.