Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 31

A viga fina, tendo uma massa de 75 kg, é suportada por dois cabos. Se o cabo na extremidade B é cortado, de modo que a viga seja liberada do repouso quando θ = 30 ° , determine a velocidade com que a extremidade A atinge a parede. Despreze o atrito em B.

Passo 1

Começaremos o exercício notando o fato de que a velocidade linear no ponto A é a mesma do centro de massa da viga, sendo assim:

v A = v G

E, com isso, a energia cinética do sistema é dada por:

T = 1 2 m v G 2 = 1 2 75 v G 2 → T = 37,5 v G 2

Passo 2

Como a viga estava inicialmente em repouso, T 1 = 0 . Através da análise das imagens a seguir, que representam o estado inicial e final da viga, respectivamente:

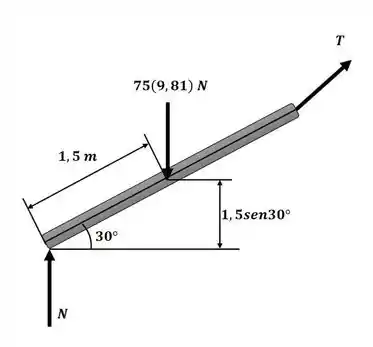
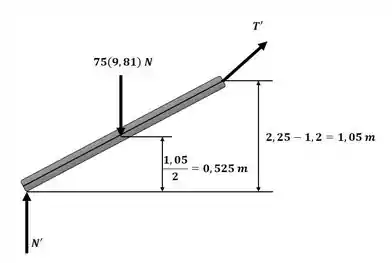
Sabemos que N e T não realizam trabalho, equanto o peso da viga realiza, sendo assim, o trabalho realizado pelo peso quando ele se desloca da posição inicial para a final é dado por:

U W = 75 9,81 0,75 - 0,525 → U W = 165,54   J

Passo 3

Agora iremos aplicar o princípio do trabalho e da energia:

T 1 + ∑ U 1 - 2 = T 2

0 + 165,54 = 37,5 v G 2

v G = 2,10   m / s = v A

Resposta

v A = 2,1   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O caixote retangular homogêneo possui uma massa de 120k g e está sustentado na posição horizontal pelo cabo em A e pela dobradiça no canto O . Se o cabo em A é liberado repentinamente, calcule a veloc
Uma haste esbelta de comprimento l e massa m está soldada na borda de um aro de raio l . Se o aro é liberado a partir do repouso na posição mostrada, determine a velocidade v do centro do aro, após te
A polia com raio de 400m m tem uma massa de 50k g e um raio de giração de 300m m . A polia e sua carga de 100k g estão suspensas pelo cabo e pela mola, que possui uma rigidez de 1,5k N / m . Se o sist
Um pequeno veículo experimental possui uma massa total m de 500k g , incluindo as rodas e o piloto. Cada uma das quatro rodas tem uma massa de 40k g e um raio de giração centroidal de 400m m . A resis
Cada uma das duas dobradiças em A e B , da tampa uniforme de massa m da caixa de brinquedos de uma criança, contém uma mola de torção que exerce um momento resistente M = K θ sobre a tampa enquanto es