Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 12
A bobina tem uma massa de e raio de giração . Se ela é liberada do repouso, determine a que distância seu centro desce pelo plano liso, antes de atingir uma velocidade angular de . Despreze o atrito e a massa da corda que está enrolada em torno do núcleo central.
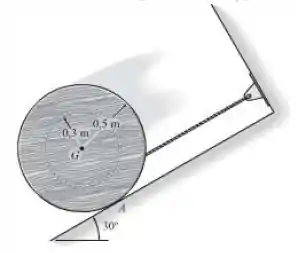
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Vejamos o diagrama cinemático:
Passo 2
Podemos aplicar o princípio do trabalho e energia analisando o momento incial e final do sistema.
Temos que:
Como o momento inicial é o repouso, temos que:
Para o momento final, temos:
Sabendo que e :
Passo 3
A parcela do trabalho , será:
Agora é só aplicar:
Resposta
Exercícios de Livros Relacionados
A barra esbelta uniforme de massa m é mostrada na sua configuração de equilíbrio antes da força P ser aplicada. calcule a aceleração angular inicial da barra após a aplicação de P .
Cada uma das barras A e B tem uma massa de 4k g e a barra C tem uma massa de 6k g . calcule o angulo assumido pelas barras se o corpo a que estão fixadas recebe uma aceleração horizontal constante α d
Montanhas-russas são projetadas de maneira que os passageiros não sintam uma força normal que seja maior do que 3,5 vezes seu peso contra o assento do carrinho. Determine o menor raio de curvatura ρ d
O esquiador parte do repouso em A e desloca-se rampa abaixo. Se o atrito e a resistência do ar podem ser desprezados, determine a sua velocidadev B quando ele chega em B . Além disso, determine a dist
O tijolo de 1 kg desliza para baixo por um telhado liso de tal maneira que quando ele está em A tem velocidade de 1,5 m/s. Determine a velocidade do tijolo imediatamente antes de ele deixar a superfíc