Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 61
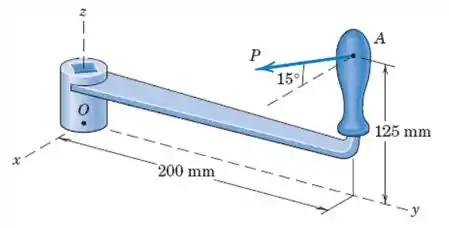
A força de módulo é aplicada na manivela da máquina estacionária, como mostrada. Escreva as reações da força e do momento em como vetores. Despreze o peso conjunto da manivela.
Passo 1
E aí meus queridxs, tudo bem com vocês?
Se liguem só, como temos uma conexão fixa ali em teremos componentes de força, ou seja, reações de forças: ; nossas forças podem ser representadas na seguinte figura
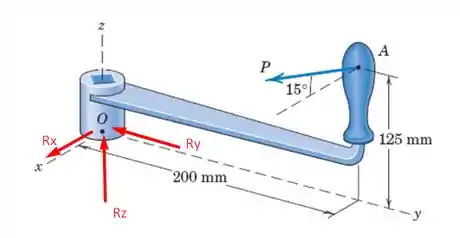
Além disso, temos um momento em cada um desses eixos no sentido positivo adotado. Pois bem, para resolvermos o problema vamos utilizar as condições de equilíbrio, a começar pelas condições de equilíbrio para a força onde teremos
Sendo assim, nosso vetor resultante pode ser escrito como sendo
Passo 2
Agora, faremos o mesmo só que utilizando as equações de momento. Então, teremos para o eixo
Seguindo para o eixo temos
Por fim, de maneira análoga, para o eixo teremos
Pronto, tá resolvido o problema. Podemos escrever nosso vetor momento como sendo