Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 3.Problemas Fundamentais - Ex. 6
Passo 1
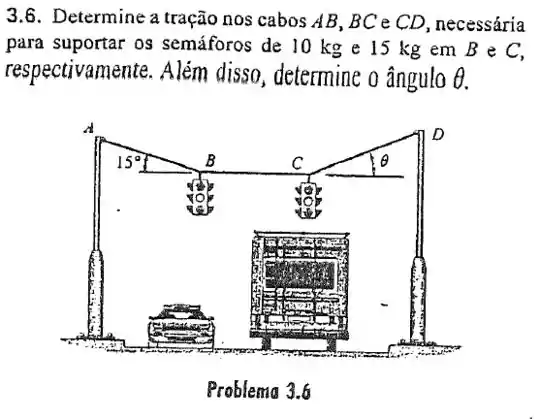
Para esse exercício devemos analisar o diagrama de corpo livre, nos nós e . Quando montarmos os diagramas sempre devemos ter cuidado para não repetir os nomes das variáveis, pois podemos confundi-las depois na hora das contas.
Nó :
Nó :
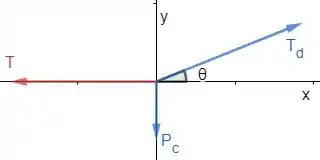
Perceba que existem dois vetores , mas nesse caso eles são iguais pois é o mesmo cabo que faz força tanto em como em .
Passo 2
A soma de forças em e em deve ser zero para os dois nós. Vamos analisar primeiro o nó :
O peso de um objeto é igual a massa dele, vezes a gravidade, então
Nós conhecemos o ângulo e a massa , substituindo:
Essa é a tração no cabo AB
Passo 3
Vamos analisar agora o eixo do nó :
Nós conhecemos o ângulo e a tração , substituindo:
Essa é a tração no cabo BC
Passo 4
Agora vamos olhar para o nó :
Eixo :
Vamos isolar alguma das duas variáveis, para substituir na equação que vamos encontrar, quando analisarmos o eixo
Passo 5
Agora vamos olhar para o eixo :
Nós temos a massa de c e temos a gravidade:
Nós sabemos também o valor de , podemos substituir na equação:
Seno sobre cosseno é igual a tangente, então
Podemos substituir esse valor de na equação:
E essa é a tração no cabo CD
Resposta
Tração no cabo AB:
Tração no cabo BC:
Tração no cabo CD: