Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 69
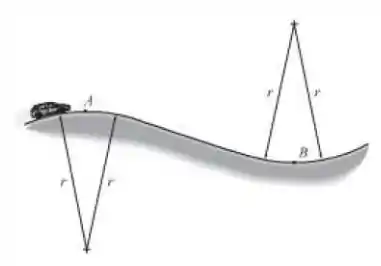
Determine a velocidade máxima na qual o carro com massa m pode passar sobre o ponto mais alto A da estrada em curva vertical e ainda manter o contato com a estrada. Se o carro mantém esta velocidade, qual é a reação normal que a estrada exerce sobre o carro quando ele passa pelo ponto mais baixo B na estrada?
Passo 1
A chave de problemas de cinética está no diagrama de corpo livre. Ao identificarmos todas as forças que o nosso problema está sujeito, conseguiremos visualizar o que há de ser feito mais facilmente.
Relembrando do capítulo de cinemática, vimos que a aceleração centrípeta de um corpo é dada por:
Precisamos resolver as equações da cinética em dois pontos distintos. No ponto A, o critério é que o carro ainda consiga manter contato com a estrada. O limite ocorre no momento em que a força normal é nula! Precisamos utilizar esta relação.
Já em relação ao ponto B, basta repetirmos as análises da cinética com o valor descoberto anteriormente.
Passo 2
Vamos começar por esboçar o diagrama de corpo livre do nosso problema. Desta forma, temos:
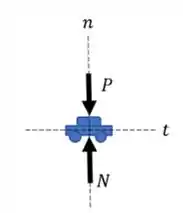
Tanto no ponto A quanto no ponto B, o carro está sujeito as mesmas forças e com as mesmas inclinações.
Passo 3
Vamos descobrir inicialmente a velocidade máxima que o carro pode passar pelo ponto A. Sabendo que a força normal é zero e ele está sujeito a uma aceleração normal, pois está em uma trajetória curvilínea, temos:
Observem que o valor da aceleração foi colocado para baixo (negativa), na direção do centro da curvatura!
Passo 4
Agora que descobrimos a máxima velocidade permitida pelo carro, precisamos repetir a nossa análise do somatório de forças na direção normal a trajetória. Só que agora temos uma pequena diferença: é no ponto B! Portanto, temos:
Observem que a aceleração está positiva pois ela aponta para cima, na direção positiva do eixo .