41. O sistema apresentado é liberado a partir do repouso de uma posição inicial. Determine o deslocamento que ultrapassa a posição de equilíbrio. Assuma um movimento de translação na direção .
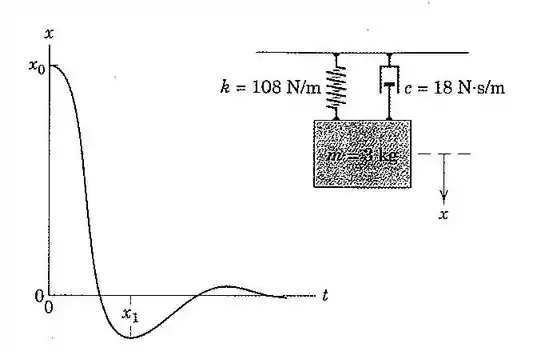
Passo 1
Primeiramente, dado que temos a nossa mola com constante elástica ; o que temos que fazer é determinar a frequência angular natural do nosso sistema, que é dada pela seguinte relação abaixo:
E substituindo os valores numéricos pertencentes a cada variável, chegamos à:
Passo 2
E agora, vamos lembrar que o fator de amortecimento está relacionado com a frequência natural e o coeficiente de amortecimento viscoso pela seguinte fórmula:
Substituindo os valores numéricos que já temos, obtemos que:
A partir desse fator de amortecimento, vamos então, tratar de obter o valor da frequência amortecida , que é dada em função da frequência natural e do fator de amortecimento , por:
Passo 3
Obtido o valor da frequência angular real do oscilador amortecido, vamos agora definir a equação de posição do nosso sistema, a qual é dada por:
O valor de nós já temos, que é a posição inicial que o corpo é liberado a partir da posição de equilíbrio. Vamos então, derivar para ver se podemos arranjar alguma coisa com a expressão da velocidade que dela advém:
Só que quando o corpo é liberado em , a velocidade é nula. Logo, nesse instante de tempo, vale zero:
Agora, vamos tratar de substituir o valor de na equação da posição de :
Só que :
Por fim, bora substituir os valores numéricos das variáveis que conhecemos, na equação acima da posição:
Já achamos a nossa equação de posição! Falta agora o tempo no qual o corpo irá ultrapassar a posição de equilíbrio. Ele é dado a partir da seguinte fórmula:
O tempo a partir do qual o corpo ultrapassa a posição de equilíbrio, é nada mais nada menos do que o tempo de meia oscilação do corpo, cujo valor é dado abaixo por:
Vamos substituir esse tempo na nossa equação da posição e finalmente acabou:
Resposta
O deslocamento que ultrapassa a posição de equilíbrio é de .