Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 96

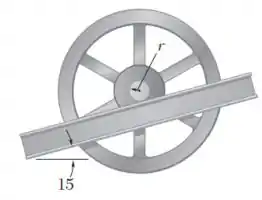
Um volante de motor de raio de giração em torno do centro de massa k é preso rigidamente a um eixo que pode rolar ao longo de trilhos paralelos. Representando por μ S o coeficiente de atrito estático entre o eixo e os trilhos, deduza uma expressão para o maior ângulo de inclinação β no qual não ocorrerá deslizamento.

Passo 1

Cinemática:

S = v 0 t + 1 2 a - t 2 16   m = 0 + 1 2 a - ( 40 s ) 2 a - ¯ = 0.02 m / s 2 ← 15 ∘ a - = r α ; 0.02 m / s 2 = ( 0.125 ) α α = 0.16 r a d / s 2

Passo 2

Cinética

+ ) Σ M C = Σ M C e f f : mgsen ⁡ β r = I - α + ( m a - ) r

mgsen ⁡ β r = m k - ² α + m r ² α

g s e n ⁡ 15 ∘ = ( k - 2 + r ² ) α

α = g r r 2 + k - 2 s e n ⁡ β + ↗ Σ F = Σ F e f f : F - m g s e n ⁡ β = - m a → F - m g s e n ⁡ β = - m r α F = m g s e n ⁡ β - m r α + ∖ Σ F = Σ F e r r : N - m g c o s ⁡ β = 0 N = m g c o s ⁡ β

Se não tem deslizamento

F = μ s N &  or  μ s = F N

μ s = F N = m g s e n ⁡ β - m r α m g c o s ⁡ β = s e n ⁡ β - r g α cos ⁡ β

Substitua para α na Eq.(1)

μ s = s i n ⁡ β - r g ⋅ g r r 2 + k - 2 s e n ⁡ β cos ⁡ β μ s = t a n ⁡ β 1 - r 2 r 2 + k - 2 = t a n ⁡ β k - 2 r 2 + k - 2 t a n ⁡ β = μ s r 2 + k - 2 k - 2

t a n ⁡ β = μ s 1 + r k - 2

Resposta

t a n ⁡ β = μ s 1 + r k - 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que no instante mostrado na figura a velocidade angular da barra BE é de 4r a d/ s no sentido anti-horário, determine (a) a velocidade angular da barra AD, (b) a velocidade do colar D, (c) a v
Sabendo que no instante mostrado na figura a velocidade do colar D é de 1,6m / s para cima, determine (a) a velocidade angular da barra AD, (b) a velocidade do ponto B, (c) a velocidade do ponto A.
A barra AB desliza livremente ao longo do chão e no plano inclinado. Deduza por v A a velocidade do ponto A , obtenha uma expressão para (a) velocidade angular da barra, (b) a velocidade da extremidad
A barra AB desliza livremente ao longo do chão e no plano inclinado. Sabendo que θ = 20 ° , β = 50 ° , l = 0,6m , v A = 3m / s , determine (a) velocidade angular da barra, (b) a velocidade da extremid
O braço ABD está conectado por pinos ao colar em B e à manivela DE. Sabendo que a velocidade do colar B é de 400m m / s para cima, determine (a) a velocidade angular do braço ABD e (b) a velocidade do