Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.4 - Ex. 41

41- Duas barras idênticas estão soldadas em um ângulo de 120 e são articulas em O , como mostrado. A massa do apoio é pequena em comparação a massa das barras. Investigue a estabilidade da posição de equilíbrio mostrada.

Passo 1

O bizu dessa questão é calcularmos o centro de gravidade dessa figura. Já que ela se trata de uma figura simétrica, rotacionada em torno de O e a distância do centro de gravidade a articulação O é constante.

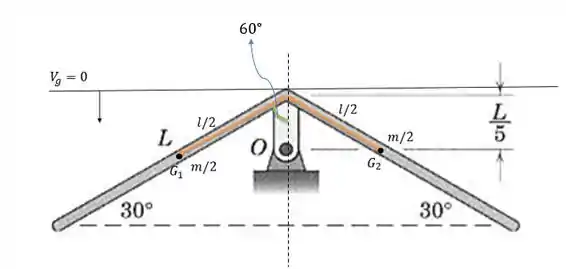
Considerado que a massa de cada barra é de m / 2 . A fórmula do centro de massa é:

y - = m 2 L 2 cos ⁡ 6 0 + m 2 L 2 cos ⁡ 6 0   m 2 + m 2 = L 4

Para calcular o centro de massa obrigatoriamente temos que espelhar a altura dele na vertical. Para isso usamos o ângulo de 60 ° que é complementar ao de 30 ° dentro do triângulo retângulo que a barra forma com o seu centro.

Passo 2

Porém nosso sistema tem como referência o ponto O e o centro de gravidade do sistema tem que incluir a articulação O que faz parte do sistema só que tem massa desprezível, como em x a figura é simétrica logo o centro de gravidade está exatamente abaixo da articulação de modo que:

Agora podemos calcular a energia potencial gravitacional do sistema que é:

V = V g = m g h

Onde h é a diferença entre o ponto O e o ponto G que é a diferença entre o menor ponto do sistema e o seu centro de gravidade(lembrando que o sistema está abaixo da linha de energia potencial gravitacional nula, então ela é negativa), logo:

h = - l 4 - l 5 cos ⁡ θ = - l 20 cos ⁡ θ

Logo a energia potencial gravitacional é:

V = - m g l 20 cos ⁡ θ

Passo 3

Derivando a energia potencial em relação a θ nós teremos:

d V d θ = m g l 20   s e n   θ

Para θ = 0 temos:

d V d θ = m g l 20   s e n   0 = 0

O que caracteriza um ponto de equilíbrio.

Logo a segunda derivada , temos:

d 2 V d θ 2 = m g l 20 cos ⁡ θ

Para θ = 0 :

d 2 V d θ 2 = m g l 20 cos ⁡ 0 = m g l 20

O que configura um sistema estável.

Resposta

Estável.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

54- O hemisfério sólido de diâmetro 2 b e o cilindro concêntrico de diâmetro b estão em repouso sobre uma superfície horizontal. Determine a altura máxima h que o cilindro pode ter sem fazer com que o
74- Calcule, em função de x , a energia potencial total ( V = V e + V g ) para a porta industrial do Prob. 7/69 e verifique o resultado dado para aquele problema. Considere V g = 0 tendo como referênc
A suspensão dianteira de eixo duplo é usada em caminhões pequenos. Em um teste do comportamento projetado, o chassi F deve ser levantado com um macaco de forma que h = 350m m , para relaxar a compress
Um suporte, em forma de paralelogramo, proposto para uma luminária ajustável é mostrado. Se o comprimento não esticado da mola é b / 2 , determine a rigidez k da mola necessária para haver equilíbrio
O pêndulo de 1,5 kg oscila em relação ao eixo O - O e tem centro de massa em G . Quando θ = 0 , cada mola tem um alongamento inicial de 100 mm. Calcule a rigidez máxima k de cada uma das molas paralel