Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.4 - Ex. 40

40- Determine, para um dado valor de θ , a força P necessária para manter o equilíbrio do mecanismo acionado por uma mola. A mola tem uma rigidez k e não está comprimida em θ = 0 . A massa dos elementos pode ser desprezada.

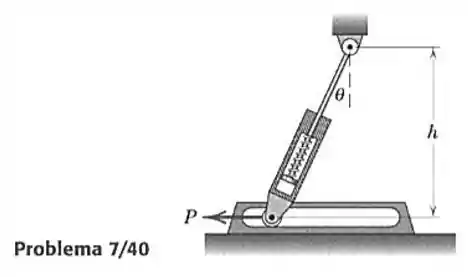
Passo 1

Por termos uma força externa P no sistema não temos outra escolha a não ser fazer direto.

δ U = δ V

E como não temos nenhum objeto com massa, então só temos a energia potencial elástica no sistema, logo:

δ U = δ V e

Passo 2

Vamos fazer o desenho do sistema com θ = 0 .

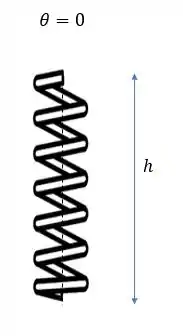
Onde vamos assumir que inicialmente a mola tem altura h . (Mesmo que não seja a compressão manterá a proporcionalidade).

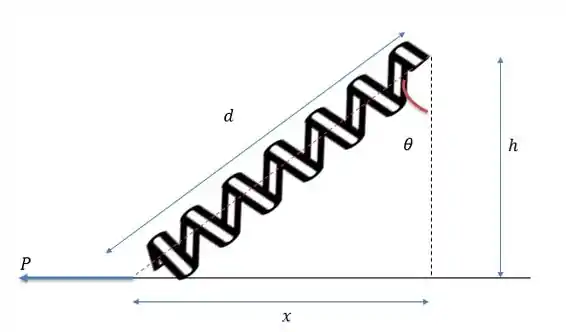
Vendo nosso ângulo θ conseguimos achar o valor de x fazendo:

t g θ = c a t e t o   o p o s t o c a t e t o   a d j a c e n t e = x h

x = h   t g   θ

E o valor de d será igual a:

cos ⁡ θ = c a t e t o   a d j a c e n t e h i p o t e n u s a = h d

d = h cos ⁡ θ

Logo nossa variação do comprimento da mola será de:

d - h = h cos ⁡ θ - h = h 1 cos ⁡ θ - 1 = h ( sec ⁡ θ - 1 )  

Passo 3

O trabalho feito pela força P será de:

P d x = P d ( h tan ⁡ θ )

Pois P tende a andar sobre a linha x .

E o trabalho feito pela força elástica será de:

K × h ( sec ⁡ θ - 1 ) × d ( h ( sec ⁡ θ - 1 )

Igualando as duas equações, temos:

P h   d ( tg ⁡ θ ) = K h 2 ( sec ⁡ θ - 1 )   d ( sec ⁡ θ - 1 )

Pela regra do quociente temos que:

d ( tg ⁡ θ ) = sec 2 ⁡ θ   d θ

E

d ( sec ⁡ θ ) = s e c θ t g θ   d θ

Substituindo então esses resultados:

P h × s e c 2 θ   d θ = K h 2 ( sec ⁡ θ - 1 ) × s e c ⁡ θ t g θ   d θ

Cortando h , sec ⁡ θ e d θ da equação temos:

P sec ⁡ θ = K h   ( t g   θ ) ( sec ⁡ θ - 1 )

Dividindo os dois lados por sec ⁡ θ   temos:

P = K h   t g   θ 1 - 1 sec ⁡ θ

Mas como sec ⁡ θ = 1 cos ⁡ θ , logo cos ⁡ θ = 1 sec ⁡ θ . Então.

P = K h ( t g   θ ) ( 1 - cos ⁡ θ )  

Resposta

P = K h (   t g   θ ) ( 1 - cos ⁡ θ )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a energia potencial para um sistema conservativo com um grau de liberdade é expressa pela relação ( V = 24 sen ⁡ θ + 10 cos ⁡ 2 θ )J , 0 ≤ θ ≤ 90 º º , determine as posições de equilíbrio e investi
A mola está livre quando θ = 45 º ºe tem uma rigidez k = 20k N / m . Determine o ângulo θ para o equilíbrio se cada um dos cilindros pesa 250 N. Despreze o peso dos membros.
Uma mesa de servir uniforme com 5 kg é apoiada em cada lado por pares de ligações idênticas , AB e CD, e molas CE. Se a tigela tem uma massa de 1 kg, determine o ângulo θ onde a mesa está em equilíbri
O cone homogêneo tem uma cavidade cônica cortada, conforme a figura. Determine a profundidade d da cavidade em termos de h de modo que o cone se equilibre sobre o pivô e permaneça em equilíbrio indife
A montagem mostrada consiste em um bloco semicilíndrico e retangular. Se o bloco pesa 40 N e o semicilindro 10 N, investigue a estabilidade quando a montagem estiver apoiada na posição de equilíbrio.