Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.4 - Ex. 44

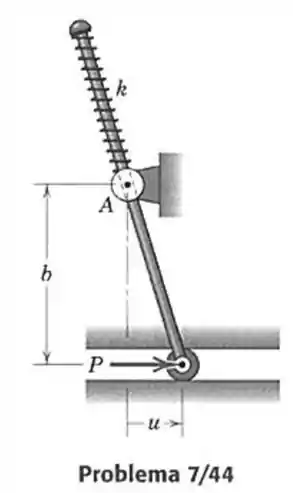
44- A mola de rigidez k não está comprimida quando u = 0 . A medida que u aumenta, a barra desliza dentro do anel articulado em A e comprime a mola situada entre o anel e a extremidade da barra. Determine a força P necessária para produzir um dado deslocamento u . Considere ausência de atrito e despreze a massa da barra.

Passo 1

A ideia é a mesma do exercício 40 , como temos uma força externa dando movimento ao objeto logo não temos escapatória senão fazer:

δ U = δ V e

Onde a energia potencial elástica é a única energia estática do sistema.

Passo 2

Vamos fazer o desenho da mola e quanto ela deve variar de tamanho indo da condição inicial até a final.

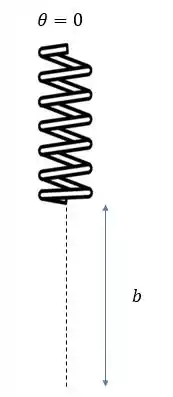
Inicialmente o tamanho complementar da barra vale b .

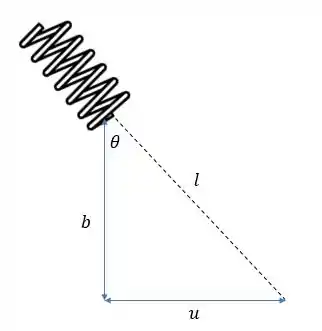
Depois de percorrido um ângulo θ em A o comprimento complementar da barra agora vale l e que tem valor igual a:

l 2 = b 2 + u 2

l = b 2 + u 2  

E como o comprimento da mola mais o comprimento desse complemento é constante pode-se dizer que a mola comprimiu um comprimento l igual a:

x = b 2 + u 2 - b

Onde x é o valor da compressão da mola.

Passo 3

Então agora se fizermos:

δ U = δ V e

Nós vamos ter:

P δ u = K x   δ x

P δ u = K b 2 + u 2 - b δ b 2 + u 2 - b

Derivando em relação a u teremos:

P δ u = K b 2 - u 2 - b 2 u 2 b 2 + u 2 δ u

Cortando δ u teremos:

P = K u 1 - b b 2 - u 2

Resposta

P = K u 1 - b b 2 - u 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os ângulos θ para haver equilíbrio do cilindro de 100 kg e investigue a estabilidade em cada posição. A mola tem uma rigidez de k = 6 k N m e um comprimento livre de 225 mm
Se uma carga l de 10 kg é colocada na panela, determine a posição x do bloco H de 0,75 kg para haver equilíbrio. A balança está em equilíbrio quando não há peso nem carga na balança.
Se o mecanismo está em equilíbrio quando θ = 30 º º, determine a massa da barra BBC. A mola tem uma rigidez k = 2 kN/m e está livre quando θ = 0 º º. Despreze a massa das ligações
O cilindro é feito de dois materiais de modo que tem uma massa m e um centro de gravidade no ponto G. Mostrre que, quando G se encontra acima do centroide C do cilindro, o equilíbrio é instável.
Determine os ângulos θ para haver equilíbrio do cilindro de 50 kg e investigue a estabilidade em cada posição. A mola está livre quando θ = 60 º º