Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 11.Problemas - Ex. 44

O cilindro é feito de dois materiais de modo que tem uma massa m e um centro de gravidade no ponto G. Mostrre que, quando G se encontra acima do centroide C do cilindro, o equilíbrio é instável.

Passo 1

Desenhando o diagrama do corpo livre

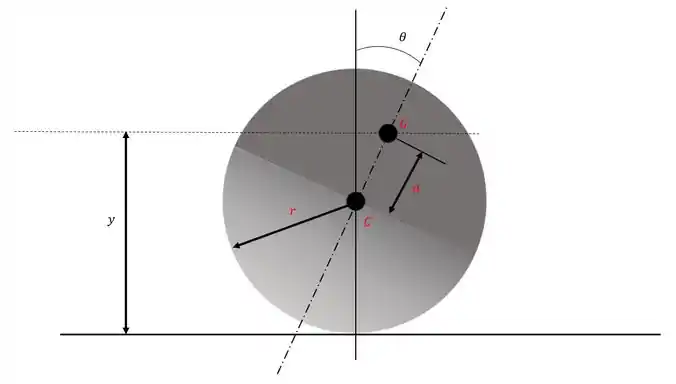
Passo 2

Da geometria da figura:

y = r + G C c o s θ y = r + a c o s θ

Passo 3

Calculando a energia potencial do cilindro: V = m . g ⋅ y V = m g ( r + a c o s θ )

Passo 4

Para calcular a posição de equilíbrio, devemos calcular a primeira derivada da função potencial:

d V d θ = m g - a s e n θ d V d θ = - m g a s e n θ = 0 ⇒ s e n θ = 0 θ = 0

Passo 5

Para verificar a estabilidade, devemos calcular a segunda derivada da função potencial:

d 2 V d θ 2 =   - m ⋅ g ⋅ a ⋅ c o s θ d 2 V d θ 2 θ = 0 = - m ⋅ g ⋅ a ⋅ c o s 0 º < 0   ;   j á   q u e   m , a , g   > 0   e   c o s 0 = 1 > 0 P o r t a n t o   o   e q u i l í b r i o   é   i n s t á v e l ,   c o m o   q u e r í a m o s   d e m o n s t r a r

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A  haste uniforme tem 80k g de massa.  Determine  o  ângulo  θ   de  equilíbrio e investigue a sua estabilade quando estiver nessa posição A mola não está deformada quando  θ = 90 ° ?
Se  a  função de potencial de um  sistema conservativo com um grau de liberdade é  V = ( 10 cos ⁡ 2 θ + 25 sin ⁡ θ ) J , onde  0 °θ180 ° , determine as posições de equilíbrio e investigue a estabilida
A pequena balança postal consiste em um contrapeso W 1 , conectado aos elementos que possuem peso desprezível. Determine o peso W 2 que está na bandeja em termos dos ângulos θ e ϕ e das dimensões most
A haste uniforme A D tem 20k g de massa. Se a mola conectada não está deformada quando θ = 90 ° , determine o ângulo θ para haver equilíbrio. Observe que a mola sempre permanece na posição vertical, e
Cada elemento tem uma massa por comprimento m 0 . Determine os ângulos θ e ϕ nos quais eles estão suspensos em equilíbrio. O contato em A é liso, e ambos são conectados por um pino em B .