Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 12
Prove que a frequência natural de oscilação da massa independe de .
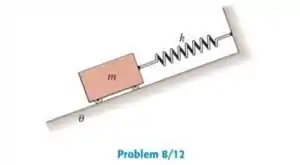
Passo 1
Vamos tomar as coordenadas com a mesma inclinação que o plano, com a origem no centro de massa do bloco quando está na posição de equilíbrio, dessa forma, a força normal estará na direção de y, e a força da gravidade terá um desvio em relação ao eixo y.
Passo 2
A componente no eixo x da força gravitacional será:
E a força elástica da mola:
Onde é a força peso do bloco na situação de equilíbrio, onde kx é 0:
E pela segunda lei de Newton para o eixo x:
E, portanto:
Passo 3
Pela equação da frequência natural, que será igual à raiz do termo que está multiplicando o x:
Convertendo para :
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
134. O instrumento sísmico mostrado está fixado no convés de um navio próximo da popa, onde a vibração induzida pela hélice é mais pronunciada. O navio possui uma única hélice com três pás que gira a
133. O cilindro A de raio r , massa m , e o raio de giração k é acionado por um sistema cabo-mola fixado ao cilindro acionador B , que oscila conforme indicado. Se os cabos não deslizam sobre os cilin
127. Determine o período τ para pequenas oscilações do conjunto composto por duas barras leves e duas partículas, cada uma de massa m . Examine a sua expressão quando o ângulo α se aproxima dos valore
131. Calcule o fator de amortecimento ζ do sistema apresentado, se a massa e o raio de giração do cilindro escalonado são m = 8k g e k = 135m m , a constante de mola é k = 2,6k N / m , e o coeficiente
136. Um motor experimental de 220k g está montado sobre um banco de ensaios com suportes elásticos em A e B , cada um com uma rigidez de 105k N / m . O raio de giração em relação a seu centro de massa